一次関数の定点公式を現役高校生がわかりやすく解説！【中2数学】

こんにちは、Daddyです。

突然ですが、\(xy\)平面上で、傾きが\(a\)で\((2, 4)\)を通るグラフの式をすぐに表せますか？

\(y=ax+b\) に \(x=2, y=4\) を代入して \(b\) を求めて……とすると、非常にめんどくさいです。

コレを解決してくれるのが、定点公式と呼ばれる破壊力バツグンの公式。

これを用いると、先ほどの答えが \(y=a(x-2)+4\) とすぐに求めることができるのです。

今回は、1次関数の計算を飛躍的にわかりやすくしてくれる公式を解説します。

定点公式

定点公式は、1点の座標が与えられれば、そこを通る全ての直線を表せるという公式です。

日本語だと理解するのがやや難しいので、下の公式を眺めた上で、例題を解いてみましょう。

ここでは2通りの解法を示します。

いずれも非常に重要ですが、試験本番では定点公式を用いるのが望ましいです。

『え？これだけ？』と思いましたか？

定点公式を使えば、代入するだけで問題を解き終えることができます。

この公式は、特に『傾きが文字で表されているとき』に有効です。

冒頭の問題を、ぜひ2通りで解いてみてください。

定点公式のありがたみがわかります。

---

ここまでが、定点公式の説明になります。

あとは問題演習を通して暗記するだけですが、なぜこの公式が成り立つのか、気になる人もいますよね。

以降の記事では、背伸びしてちょっとだけ高校数学をかじってみましょう。

暗記に頼ることなく、おのずと理解が深まります。

もちろん、中学生を対象に解説します。

グラフの平行移動

なぜ『平行移動』を扱うのか

いきなり『グラフの並行移動』というフレーズが登場しました。

実はこの内容は高校数学の分野になりますし、高校でさえ結果を教わるだけで証明を扱わないくらい無視される分野なのですが、本来非常に大事な内容です。

定点公式は、この『グラフの平行移動』の1次関数バージョンに他なりません。

証明はやや理解しづらいですが、それを除けば決して難しい内容ではありません。

公式の暗記もラクになること間違いありませんから、チャレンジすることを強くオススメします。

グラフの平行移動の公式

グラフの平行移動の公式は、下のように表現されます。

この時点では理解できなくても構いませんが、なんとなく定点公式に似ているなー、ということがわかってくれれば良いです。

ここで登場した \(f(x)\) は、超簡単に言えば、\(x\) が使われた式全般を表します。

\(f(x)\) が何か知りたい人は、下の記事をどうぞ。

一次関数の右辺のように \(f(x)=4x+3\) と表されることもありますし、反比例のグラフの右辺のように \(f(x)=\dfrac{6}{x}\) と表されることもあります。

具体例を見て、この公式の意味を理解してみましょう。

前提ですが、これは高校数学の中でも理系の人しか学ばない『数学Ⅲ』の『分数関数』という分野を噛み砕いて説明していますから、理解できなくても落ち込む必要はありません。

目的は、定点公式を理屈で覚えるということです。

\(x\)軸方向に-2だけ動かすなら、\(x\)から-2を引き算し、\(x\)軸方向に3だけ動かすなら、\(y\)から3を引き算するということです。

なぜ『引き算』なのか、というのは割愛しますが（文字を多用して証明するので、中学生には理解が難しい）、とにかく平行移動する分だけ引き算するという事実を覚えてください。

これは面白いことに、どのようなグラフでも成立することが証明されています！

定点公式の証明

\(y=ax\) のグラフを、\((\Box, \bigcirc)\)を通るように平行移動させましょう。

\(y=ax\) のグラフは原点を通るので、原点 \((0, 0)\) を \((\Box, \bigcirc)\) へと平行移動させればよいですね。

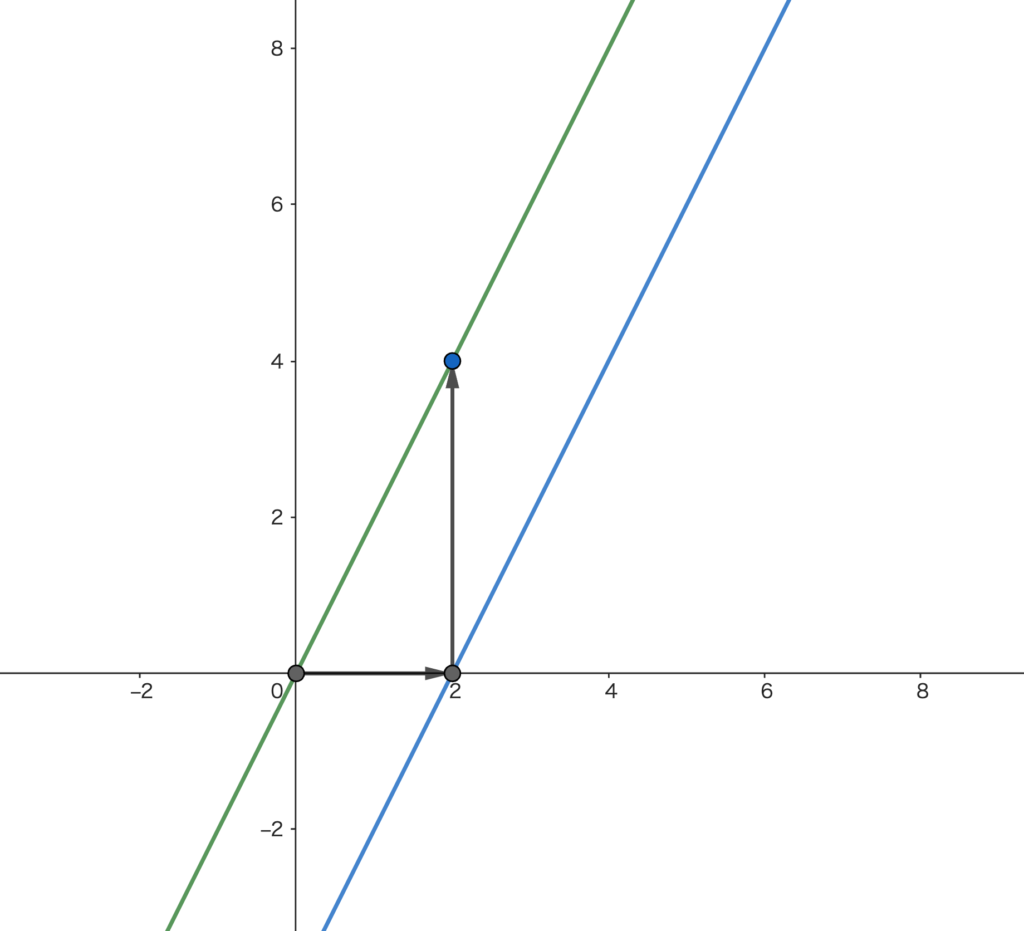
平行移動の公式に代入して、\(y-\bigcirc=a(x-\Box)\)というわけ。

まとめ

いかがだったでしょうか？

定点公式は必須の公式ではないということもあってか、中学校の義務教育では教わりません。

しかし、今後高校受験などで複雑な問題を解く際、定点公式は当たり前のように出現してきます。

『この記事を読めてラッキー！』と思って、絶対にマスターしてください。

また、平行移動の内容は発展内容なのでカンペキに理解する必要はありませんが、雰囲気がつかめているだけでも今後の数学力は大幅に向上してきます。

それではっ！