
こんにちは。整数問題が大好きなDaddyです。
今回は、合同式というものについて語ろうと思います。
残念ながら、日本では合同式を学ぶ機会はほぼありません。
ほとんど全ての教科書から、整数問題が削除されてしまったからです。
それでも、整数問題は数学のキホン中のキホンなので、入試問題には出るだろうし、何より勉強すること自体に意味があります。
とっても楽しい分野ですから、早速勉強しましょう!
数学の世界を考える
見方を変えた世界
ここからは、数学がニガテな方のために、導入をゆっくり丁寧にしていきます。つまらないと思われる方は、目次から『合同式』に直接とぶようにしてください。
まずは導入として、数学の世界そのものについて考えてみましょう。
数学では、属する世界が変わると、ものの見方や考え方、表し方など、何もかもが大きく変わります。
例えば、10進法が挙げられますね。
私たちは便宜上、\(0,1,2,3,4,5,6,7,8,9\) という10この数字を使って数を表現していきます。
ところが、この10進法が本当に便利なのかどうかは、わかりません。
例えば、\(\dfrac{1}{3}\) という数を小数で表そうとすると、\(0.3333 \cdots\) となり、不便ですよね。
3進法ならどうでしょう。
実は、3進法なら同じ数を \(0.1\) と表すことができます。(重要ではないので、その理由は省略)
こんな感じで、数学は表記ひとつで世界がガラリと変わります。
拡張した世界
世界を広げることだってできます。
幼い頃は誰だって、\(1, 2, 3, 4, 5, \cdots\) といった自然数と、\(0\) という数しか知らなかったはずです。(まとめて非負整数と言ったりもしますが)
やがて、万、億、兆、京…と大きい数を学び、小数や分数といった半端な数、マイナスの概念、分数ですら表すことのできない \(\sqrt{2}, \pi\) といった無理数、やがては存在すらしない虚数まで習うのです。
上に書いたものの他にも、数には様々な分類があり、分類の仕方次第で、いくらでもこの世界を広げることができそうです。
数をわり算の余りで分類する
今回の舞台は、全ての整数を『わり算の余り』で分類する、そんな世界です。
例えば、全ての整数を6で割った余りで考える世界を考えましょう。

31って数を使いたいなー

19って数を使いたいなー
こんな2人がいたとしましょう。
どちらの数も、6で割ると余りが1になります。
この世界では、31も19も同じ数だ!というふうに考えます。
極端な話、\(31=19\) みたいな表現をするです。
(上の表記は間違っています。あとで正しい表記を教えます。)

27って数を使いたいなー
この数は6で割ると余りが3ですから、31や19とは異なる数だ!と考えます。
このように全ての整数について考えていくと、6で割った余りにしたがって、6つに分類することができます。
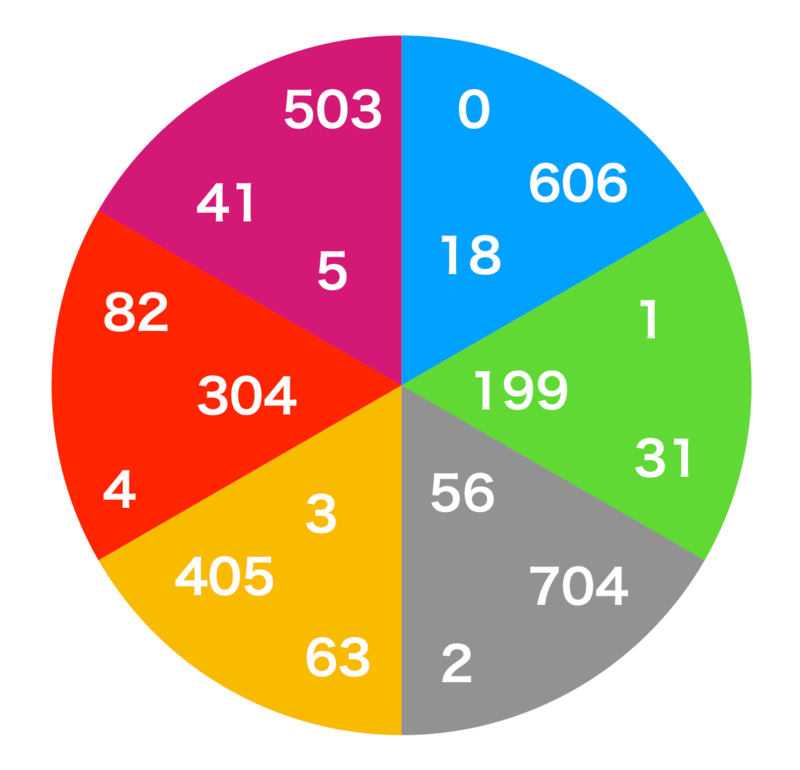
イメージは、上のような感じ。
右上の \(0, 18, 606\) という3つの数は、この世界においては同じ数とみなします。
合同式
さて、それではこの世界を数学的に表現していきましょう。
先ほどの世界では、6という数を基準に余りを考えていきました。
このように、余りの基準とする数を法と言います。
世界の基準が法である、みたいなイメージですかね。
要するに『割る数』のことです。
ちなみに表記は\(\pmod 6\) のように書きます。
また、先ほどの例では、31と19が同じ数であるとみなされます。
このような関係を、31と19は合同であると言います。
31と19はイコールで結ぶことはできないので、合同の記号である \(\equiv\) を用いて、\(31 \equiv 19\) のようになります。
通常、これらをまとめて表記します。数式の表現も日本語の表現も覚えましょう。
31と19は、6を法として合同である。
\(\iff 31 \equiv 19 \pmod 6\)
一般化すると、下のようになる。
\(a, b\) は、\(n\) を法として合同である。
\(\iff a \equiv b \pmod n\)
計算のルール
合同式には、方程式に似た計算のルールがあります。
結論からいうと、フツウのわり算だけができません。
それでは、ルールを丁寧にみていきましょう。
たし算
まず、合同式では両辺に同じ数を足すことができます。
\begin{eqnarray}
31 &\equiv& 19 \pmod 6\nonumber\\
31 + 2 &\equiv& 19 + 2 \pmod 6 \nonumber\\
\end{eqnarray}
一般的には、次のように表されます。
\(a \equiv b \pmod p\) のとき$$a+c \equiv b+c \pmod p$$
ひき算
同じように、合同式では両辺から同じ数を引くことができます。
\begin{eqnarray}
31 &\equiv& 19 \pmod 6\nonumber\\
31 – 2 &\equiv& 19 – 2 \pmod 6 \nonumber\\
\end{eqnarray}
一般的には、次のように表されます。
\(a \equiv b \pmod p\) のとき$$a-c \equiv b-c \pmod p$$
かけ算
同じように、合同式では両辺に同じ数をかけることができます。
\begin{eqnarray}
31 &\equiv& 19 \pmod 6\nonumber\\
31 \times 2 &\equiv& 19 \times 2 \pmod 6 \nonumber\\
\end{eqnarray}
一般的には、次のように表されます。
\(a \equiv b \pmod p\) のとき$$ka \equiv kb \pmod p$$
べき乗
二項定理などを利用すれば、べき乗でも合同式が成立することが証明できます。
ここでは結論だけ。
\begin{eqnarray}
31 &\equiv& 19 \pmod 6\nonumber\\
31^2 &\equiv& 19^2 \pmod 6 \nonumber\\
\end{eqnarray}
一般的には、次のように表されます。
\(a \equiv b \pmod p\) のとき$$a^n \equiv b^n \pmod p$$
わり算
最後にわり算ですが、これがなかなか厄介です。
\(ka \equiv kb \pmod p\) が成立しているとしましょう。
今、両辺を共通の因数 \(k\) で割りたくて、いてもたってもいられない気分ですよね(?)
ところが、\(k\) で割ってもよいのは、合同式modにおける法 \(p\) と互いに素であるときだけです。

ちょっと何言ってるか分からねえ
こんな人は、合同式でわり算するのはやめてください。マジで。
合同式でわり算できなくて困る問題は、ここだけの話、ありません。
一応、一般的には、次のように表されます。
\(ka \equiv kb \pmod p\) かつ \(k, p\) が互いに素のとき$$a \equiv b \pmod p$$
合同式のとんでもない威力
じゃ、合同式って何に使えるんでしょうか?
合同式は、シンプルなカタチをした整数問題で使うことができます。
特に、2乗、3乗といったカタチに強いです。
なぜなら、合同式の計算をいかすことで、\(0, -1, +1\) といったカタチに変形できたら、計算がめちゃくちゃカンタンになるからです。
まずは、例題をみていきましょう。
\(7^{100}\) の一の位の数を求めよ。
\(7^{100}\) は85桁ですから、絶対に計算したくありません。
85桁がどれだけ大きい数か、もはや想像すらつきませんからね。
さて、『一の位の数を求める』という日本語を数式に変換してみましょう。

10で割った余りや!
ということで、余りをmodで計算していこうと思います。
- Step1modで数式を立てる
今回求める値は、10で割った余りであるから、$$7^{100} \equiv \Box \pmod {10}$$のように変形できればよい。
- Step2無理やり-1をつくる
ここがポイント。
\(7^{100}\) をうまく変形して、10で割った余りが \(0, -1, +1\) になるようにする。
\(7^{100}\) は \((7^2)^{50}=49^{50}=(50-1)^{50}\) と変形できる。
ここで、50-1の50の部分は10の倍数だから、削除できる。
従って、\(7^{100} \equiv (-1)^{50} \pmod{10}\) - Step3整理する
\((-1)^{50}=1\) だから、$$(-1)^{50}\equiv 1 \pmod{10}$$ゆえに、求める余りは1
なんか難しそうな問題を、一瞬で解くことができました。
ここで、modの問題では非常に有効な知識があるので、伝授します。
それはズバリ、下の2つです。
3を法として、$$n^2 \equiv 0または1$$
4を法として、$$n^2 \equiv 0または1$$
何がすごいの?って感じかもしれませんが、よく考えてみてください。
3で割った余りって、フツウ \(0, 1, 2\) の3パターンですよね?
ましてや4で割った余りって、フツウ \(0, 1, 2,3\) の4パターンです。
でも、2乗した数だと余りが \(0,1\) にしかならないんです。
ちなみに証明自体はとてもカンタンなので、ぜひ自力でやってみてください。
さて、次の例題を考えてみましょう。
\(a^2+b^2+c^2=88\) となるような自然数 \(a, b, c\) を全て求めよ。
1から順番に代入したら、めっちゃ時間がかかりそうな問題です。
でも皆さんなら大丈夫。
この式の最大の特徴は『2乗だらけ』ということです。
はい、ゼッタイに合同式の問題です。
解答は下に隠しておきます。難しくないけど長いです。
- Step1とりあえずmod4
88が4の倍数なので、mod3より先にmod4で試してみよう。
以下、法を4として考える。
\((右辺) \equiv 88 \equiv 0\)
したがって、\((左辺) \equiv 0\)\(a^2, b^2, c^2\) は4で割った余りが0か1なので、\((左辺) \equiv 0\) を満たすのは \(a^2 \equiv b^2 \equiv c^2 \equiv 0\) のとき。
- Step2別の文字におきかえる
\(a^2 \equiv b^2 \equiv c^2 \equiv 0\) になるのは、\(a, b, c\) がいずれも偶数のとき。\(a=2p,\) \(b=2q,\) \(c=2r\) とおきかえる。ただし、\(p, q, r\) は自然数。
よって、
\begin{eqnarray}
&&a^2+b^2+c^2=88\nonumber\\
&&(2p)^2+(2q)^2+(2r)^2=88\nonumber\\
&&p^2+q^2+r^2=22\nonumber\\
\end{eqnarray} - Step3とりあえずmod3
22は3で割り切れないが、mod3でもなんかいけそうな気がする。
以下、法を3として考える。
\(p^2+q^2+r^2=22\)
\((右辺) \equiv 22 \equiv 1\)
したがって、\((左辺) \equiv 1\)\(p^2, q^2, r^2\) は3で割った余りが0か1なので、\((左辺) \equiv 1\) を満たすのは \(p^2, q^2, r^2\) のうち1つが余り1で、2つが余り0になるとき。
例えば、\(p^2 \equiv 1,\) \(q^2 \equiv r^2 \equiv 0\)あとで入れ替えればよいから、\(p^2 \equiv 1,\) \(q^2 \equiv r^2 \equiv 0\) で考える。
- Step4ぜんぶ書き出す
\(q^2, r^2\) を考える。mod3で0になる2乗の数は、\(3^2, 6^2, 9^2\) などがある。ただ、\(p^2+q^2+r^2\) の値である22を超えてはいけないから、\(3^2\) しか使えない。
\(q=r=3\) のみが答えになる可能性がある。
- Step5p, q, rを求める
\(p^2+3^2+3^2=22\) より、\(p^2=4\)
これは、\(p^2 \equiv 1 \pmod 3\) を満たす。よって、\((p, q, r)=(2, 3, 3)\)
- Step6a, b, cを求める
\(a=2p,\) \(b=2q,\) \(c=2r\) だから、
\((a, b, c)=(4, 6, 6)\) - Step7入れ替える
注意。答えは入れ替えても成立する。よって、
\begin{eqnarray}
(a, b, c)&=&(2, 3, 3)\nonumber\\
&=&(3,2,3)\nonumber\\
&=&(3,3,2)\nonumber\\
\end{eqnarray}
まとめ
いかがだったでしょうか?
ここまで読んでくれた方、本当にありがとうございます。
相当大変だったと思います。
でも、合同式を使いこなすことができれば、本当に強くなると思います。
幸いなことに、合同式についての解説YouTubeなどは、検索すればめちゃくちゃたくさん出てくるので、興味があればぜひ調べてみてください。
Frontiestaの問題じゃどうしても物足りないっていう人は、下の参考書がおすすめ。(難しいことで有名)
Frontiestaの記事で復習するのもお忘れなく!
それではっ!



コメント