
三平方の定理をご存じだろうか。
中学数学、図形の分野で最も難しく、最も楽しい定理。
この定理自体は簡単で、覚えやすいので早いうちから覚えていて損はない。
今回は、そんな三平方の定理をわかりやすく解説する回。
三平方の定理とは?
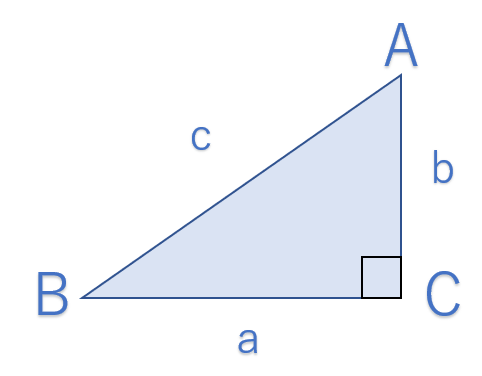
三平方の定理とは上の図のような直角三角形において、
$$c^2 = a^2 + b^2$$
の関係が成り立つことを言います。
また、古代ギリシアの哲学者であったピタゴラスという人
が発見した定理なので、「ピタゴラスの定理」とも呼ばれています。
三平方の定理の証明
今回は中学校で習う“相似”を使った証明をします。
証明)
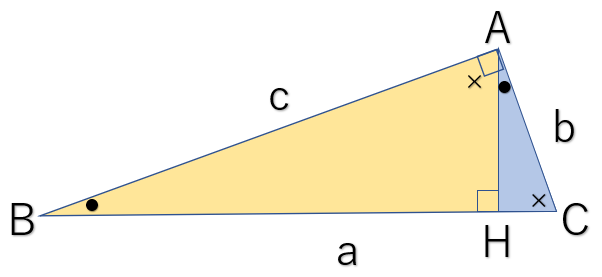
直角三角形ABCの頂点Aから辺BCに下した垂線の足をHとおく。すると、
2組の角がそれぞれ等しいので、
$$\triangle ABC \backsim \triangle HBA \backsim \triangle HAC・・・①$$
ここで分かりやすくするために相似の三角形を下に整理した。
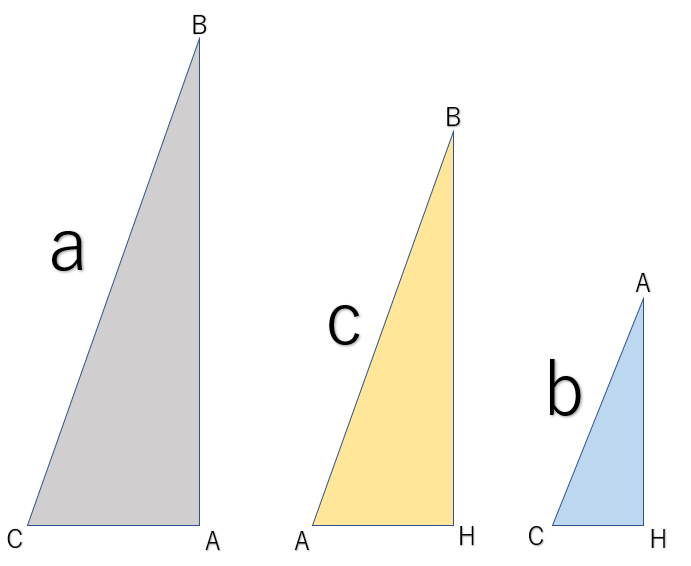
①よりこれらの三角形の相似比は、
$$a : b : c$$
よって、これらの三角形の面積比は、
$$a^2 : b^2 : c^2 ・・・②$$
そして、
$$\triangle ABC = \triangle HBA + \triangle HAC ・・・③$$
②、③より
$$a^2 = b^2 + c^2$$
証明完了
本来はさらに多くの証明方法が存在しますが、今回はあくまで
ざっくりとしたイメージをつかんでほしいので、
興味があったら調べてみてください。
問題演習
では、実際の問題を通してより理解を深めましょう。
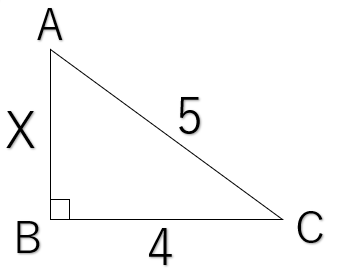
xの長さを求めよ。
三平方の定理より、
$$5^2 = 4^2 + x^2$$
$$\iff x^2 = 9$$
$$\iff x= \pm 3$$
x>0よりx=3
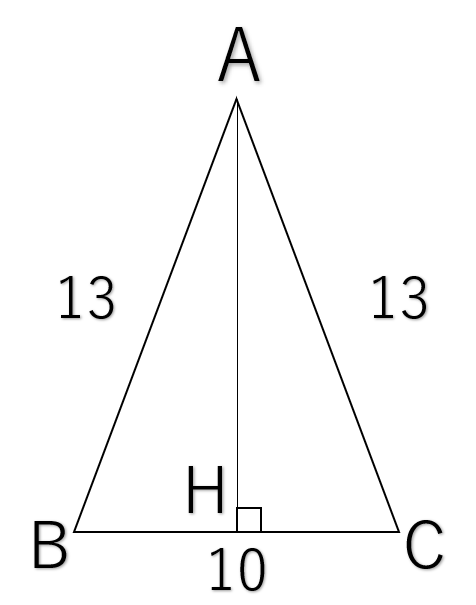
AB=AC=13
BC=10
である、
二等辺三角形ABC
の面積を求めよ。
二等辺三角形の性質から、頂点Aからおろした垂線は底辺BCを二等分するので、
BH=HC=5
ここで、三平方の定理から、
$$AH^2=13^2-5^2$$
$$⇔AH=12( \because AH \gt 0)$$
よって、求める面積は
$$10×12÷2=60$$
まとめ
最後に、三平方の定理の定義式のおさらいです。
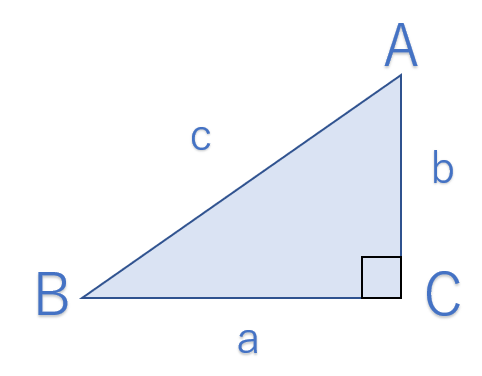
上の図の直角三角形において、
$$a^2 + b^2 = c^2$$
の関係が成り立つことを言います。
三平方の定理は、図形の問題で使わない問題はない
というほどよく使われる定理です。
これを機に完璧に自分のものにしましょう。
下はおすすめの問題集です。参考程度にどうぞ。



コメント