

こんにちは。Daddyです。
今回は、隣接3項間漸化式について扱います。

ナニそれ?美味しいの?
はい、出題されたら非常においしい単元です。
カタチだけ見てみましょう、こんなヤツ。
$$a_{n+2}=a_{n+1}+6a_n$$

\(n,n+1,n+2\)って3つも項があるね。
一体、どうやって解くのでしょうか?
慣れたらとっても楽しい単元なので、ぜひ気楽に読んでください。
それでは早速、Let’s go!
特性方程式による解法
特性方程式のご紹介

まずは、隣接3項間漸化式には特性方程式が存在する、ということを覚えましょう。

特性方程式ってなんだっけ?

特性方程式については、Frontiestaの別の記事で解説してるで。
特性方程式がわからないと、この記事の内容の99.9%は理解できません。
忘れてしまった人は下の記事を先に読んでくださいね。
さて、話をもとに戻しましょう。
隣接3項間漸化式の特性方程式は、2次方程式になります。
一旦、例題を見てみましょう。
\(a_1=1, a_2=1, a_{n+2}=a_{n+1}+6a_n\) によって定められる数列 \(\{a_n\}\) の一般項を求めよ。

さっき、導入で見た漸化式だね。
この特性方程式は、\(x^2=x+6\) になります。
漸化式とカタチを比較してみましょう。
\begin{array}{ccccc}
a_{n+2} & = & a_{n+1} & + & 6a_n\\
x^2 & = & x & + & 6
\end{array}
\(a_n\) を \(x\) で置き換えるイメージです。
\(a_{n+2} \rightarrow x^2, \ a_{n+1} \rightarrow x, \ a_n \rightarrow 1\) です。
それでは、特性方程式を解いていきます。
\(x^2=x+6\) を因数分解して解を求めるだけですね。
\(x=3, -2\) となります。
ここから難しくなります。
『なんで?』っていう変形が多くなりますが、後でまとめて証明するので、一旦やり方だけ覚えてください。

そもそも、特性方程式ってなんのために解くんやったっけ?復習やで?

等比数列に変形するためだったね。
その通り。
そのままでは解くことができない漸化式を、無理やり等比数列に変形することができれば良いのでした。
まずは、ゴールをお見せしますね。
等比数列の変形は、2通り登場します。
\begin{eqnarray}
\left\{
\begin{array}{l}
\color{red}{a_{n+2}-3a_{n+1}}\color{black}{=-2}\color{red}{(a_{n+1}-3a_n)}\\
\color{green}{a_{n+2}+2a_{n+1}}\color{black}{=3}\color{green}{(a_{n+1}+2a_n)}
\end{array}
\right.\notag
\end{eqnarray}
2つの式は、整理すると \(a_{n+2}=a_{n+1}+6a_n\) という元の漸化式に戻ることを確かめてください。
そして、\(\color{red}{b_{n+1}}\color{black}{=-2}\color{red}{b_n}, \color{green}{c_{n+1}}\color{black}{=3}\color{green}{c_n}\) のように、等比数列のカタチに変形できていることも確かめましょう。

ダメだ、難しい…

まずは、色がついているところが対応しているということを理解しよか。丁寧に音読したら理解できるかもしれんで。
確かに、この等比数列を解けばうまく解けそうです。

やっと言ってることが理解できた!
でも、どうやってこの変形を思いつくの?

そのための特性方程式やろ?
実際に、特性方程式の解を使うと、等比数列のカタチに変形できます。
分かりやすくするために、特性方程式の解を \(x=\color{#ff8c00}{3}\color{black}{,} \color{blue}{-2}\) と色をつけます。
すると、漸化式 \(a_{n+2}=a_{n+1}+6a_n\) を次のように変形できます。
\(a_{n+2}- \color{#ff8c00}{3} \color{black}{a_{n+1}=}\color{blue}{-2}\color{black}{(a_{n+1}-}\color{#ff8c00}{3}\color{black}{a_n)}\)
\(a_{n+2}- (\color{blue}{-2} \color{black}{)a_{n+1}=}\color{#ff8c00}{3}\color{black}{(a_{n+1}-(}\color{blue}{-2}\color{black}{)a_n)}\)

もしかしてこの変形、丸暗記??
そんなことはありません。
解が係数に使われているなー、ということがわかれば大丈夫です。
符号とかは、後で調整すれば良いのでね。
実際には、一発でここまで綺麗に変形するのではなく、次のような試行錯誤を踏んでいます。
- Step1テンプレートを用意する
\(a_{n+2}-\bigcirc a_{n+1} = \triangle(a_{n+1}- \bigcirc a_n)\) としておく。これは問題をたくさん解けばいずれ覚えるはず。
- Step2\(\bigcirc\) に解をぶっ込む
\(x=3, -2\) をぶっ込む。
\(a_{n+2}-3 a_{n+1} = \triangle(a_{n+1}- 3 a_n)\)
\(a_{n+2}+2 a_{n+1} = \triangle(a_{n+1}+2 a_n)\)みたいに、普通は2つできる。符号はマイナスになっているのが正しいが、どうせ検算するんだから、最悪覚えなくていい。
- Step3\(\triangle\) を適当に決める
展開したら元の漸化式に戻ってくれるような数をひたすらに代入すればいい。どうせ検算するんだから、覚えてなくていい。
\(a_{n+2}-3 a_{n+1} = -2(a_{n+1}- 3 a_n)\)
\(a_{n+2}+2 a_{n+1} = 3(a_{n+1}+2 a_n)\)が正解。
ということで、2つの等比数列ができました!
次は、それぞれの等比数列を解いていきましょう。
途中式は下のアコーディオンボックスを開いて見ることができます。
(1) \(a_{n+2}-3 a_{n+1} = -2(a_{n+1}- 3 a_n)\) を解く。
\(b_n=a_{n+1}- 3 a_n\) とおくと、\(b_{n+1}=-2b_n\) となり、等比数列である。
\(b_1=a_2-3a_1=-2\) より、初項-2, 公比-2であるから、\(b_n=(-2)^n\)
したがって、\(a_{n+1}- 3 a_n=(-2)^n\)
(2) \(a_{n+2}+2 a_{n+1} = 3(a_{n+1}+2 a_n)\) を解く。
\(c_n=a_{n+1}+2 a_n\) とおくと、\(c_{n+1}=3c_n\) となり、等比数列である。
\(c_1=a_2+2a_1=3\) より、初項3, 公比3であるから、\(b_n=3^n\)
したがって、\(a_{n+1}+2 a_n=3^n\)
上の計算から、2つの漸化式が得られましたね。
\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}- 3 a_n=(-2)^n \\
a_{n+1}+2 a_n=3^n
\end{array}
\right.\notag
\end{eqnarray}

さあ、仕上げやで。どうやって\(a_n\)を求めようか?

ズバリ、さらに2つとも漸化式を解く!

残念!もっと楽に計算できるで
さっきの2つの漸化式、どこか見覚えがあるような形をしていますよね。
そう。連立方程式です。
\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}- 3 a_n=(-2)^n \quad \cdots (1)\\
a_{n+1}+2 a_n=3^n \quad \cdots (2)
\end{array}
\right.\notag
\end{eqnarray}
\(a_{n+1}=x, a_n=y\) と置き換えると、
\begin{eqnarray}
\left\{
\begin{array}{l}
x- 3 y=(-2)^n \\
x+2 y=3^n
\end{array}
\right.\notag
\end{eqnarray}
もちろん、慣れたら \(x,y\) で置き換える必要はありません。
とにかく、単に \(a_n\) を直接求めれば良いのです。
さて、上の式番号で(2)-(1)を計算すると、\(a_{n+1}\) が消去できます。
\(5a_n=3^n-(-2)^n\)
\(\therefore a_n=\dfrac{3^n-(-2)^n}{5}\)

やっと答えが出た!
おめでとうございます!
ちなみに、特性方程式は記述答案に書く必要はありません。
いきなり式変形をしてしまって良いです。
この特性方程式の使い方は、しっかりマスターしてしまってください。
もう一回例題を解けば習得できるはずです。
特性方程式の証明

さて、そろそろ疲れてきた頃だと思いますが、特性方程式が使える理由を解説します。
それでは結論!たまたま成功するだけ!

と、とうとう頭がおかしくなっちまったか…
いや、そういうわけではなくてですね。
特性方程式っていうもの自体が、たまたま成功するものなんですよ。
とはいえ、数式でもしっかり証明した方がいい気がするので、やっておきます。
\(a_{n+2}+pa_{n+1}+qa_n=0\) という漸化式について考える。
この漸化式が次のように、等比数列のカタチに整理できるものとする。
\(a_{n+2}- \alpha a_{n+1}= \beta (a_{n+1} -\alpha a_n)\)
この式中の \(\alpha, \beta\) が、特性方程式 \(x^2+px+q=0\) の2解であることを証明すれば良い。
\begin{eqnarray}
&a_{n+2}- \alpha a_{n+1}= \beta (a_{n+1} -\alpha a_n)\nonumber\\
&a_{n+2}- \alpha a_{n+1}= \beta a_{n+1} -\alpha \beta a_n\nonumber\\
&a_{n+2}- \alpha a_{n+1} – \beta a_{n+1} +\alpha \beta a_n=0\nonumber\\
&a_{n+2}- (\alpha + \beta ) a_{n+1} +\alpha \beta a_n=0\nonumber\\
\end{eqnarray}
係数を比較すると、
\begin{eqnarray}
\left\{
\begin{array}{l}
p=- (\alpha + \beta ) \\
q=\alpha \beta
\end{array}
\right.\notag
\end{eqnarray}
特性方程式 \(x^2+px+q=0\) に代入すると、
\begin{eqnarray}
x^2-(\alpha + \beta )x+\alpha\beta =0\nonumber\\
(x-\alpha)(x-\beta)=0\nonumber\\
\end{eqnarray}
よって、\(\alpha, \beta\) は特性方程式の2解になっており、確かに証明された。
これだけですね。シンプルです。
でも、特性方程式ってかなり偉大です。
答えを予想する解法

本当は、先ほどの特性方程式さえ理解してしまえば、問題を解く上では十分です。
ですが、漸化式という単元の特性上、数学的帰納法と絡めて出題されることがあります。

面倒なことさせるんじゃねえ!
逆にいえば、答えを先に予想して、それを数学的帰納法で証明する方法もあるということ。
使える場面は限られますが、成功したらスピーディに解答できます。
答えを予想するように誘導がついていることもあるので、一応習得してみてください。
こんな問題を作ってみました。
\(a_1=3, a_2=6, a_{n+2}=a_{n+1}+2a_n\) によって定められる数列 \(\{a_n\}\) について、次の(1),(2)に答えよ。
(1) \(a_3, a_4\) を求めよ。
(2) \(\{a_n\}\) の一般項を求めよ。
まずは(1)。
これは代入して解くだけですね。
\(a_{n+2}=a_{n+1}+2a_n\) に \(n=1\) を代入する。
\begin{eqnarray}
a_3&=&a_2+2a_1\nonumber\\
&=&6+2\times3\nonumber\\
&=&12\nonumber\\
\end{eqnarray}
\(a_{n+2}=a_{n+1}+2a_n\) に \(n=2\) を代入する。
\begin{eqnarray}
a_4&=&a_3+2a_2\nonumber\\
&=&12+2\times6\nonumber\\
&=&24\nonumber\\
\end{eqnarray}
よって、\(a_3=12, a_4=24\)
続いては、(2)です。
(1)が明らかに誘導なので、これを使ってちょっと数列を眺めてみましょう。
\begin{array}{c|ccccc}
n & 1 & 2 & 3 & 4 & \cdots \\
\hline
a_n & 3 & 6 & 12 & 24 & \cdots \\
\end{array}

なんか、規則的だね。

初項が\(3\)、公比が\(2\)の等比数列になってるっぽいな。
それでは、\(a_n=3\cdot 2^{n-1}\) であると予想し、それを証明していきましょう。
$$a_n=3\cdot 2^{n-1} \ \cdots (*)$$
であることを、数学的帰納法によって証明する。
(1) \(n=1, 2\) のとき
\begin{eqnarray}
a_1=3\cdot 2^{0}=3\nonumber\\
a_2=3\cdot 2^{1}=6\nonumber\\
\end{eqnarray}
より、\((*)\)は成立している。
(2) \(n=k, k+1 \quad (k=1,2,3, \cdots)\)のとき、\((*)\)の成立を仮定する。つまり、
\begin{eqnarray}
\left\{
\begin{array}{l}
a_k=3\cdot 2^{k-1} \\
a_{k+1}=3\cdot 2^{k}
\end{array}
\right.\notag
\end{eqnarray}
が成立すると仮定する。
このとき、
\begin{eqnarray}
a_{k+2}&=&a_{k+1}+2a_k\nonumber\\
&=&(3\cdot 2^{k})+2 \cdot (3\cdot 2^{k-1})\nonumber\\
&=&3\cdot 2^{k}+3\cdot 2^{k}\nonumber\\
&=&3\cdot 2^{k+1}\nonumber\\
\end{eqnarray}
よって、\(n=k+2\) のときも\((*)\)が成立している。
(1)(2)より、数学的帰納法から\((*)\)が成立することが証明された。
ゆえに、\(a_n=3\cdot 2^{n-1}\)
こんな感じで、答えが予想できたらあとは証明するだけで構いません。
好みは人それぞれですが、私はこちらの方が好きです。
とはいえ、どちらの方法でも解けるようにしておいてくださいね。
おまけ

3項間漸化式ってなんかの役に立つの?

んー、それ言われたらきついなー。フィボナッチ数列とか?
数学好きなら全員が知っている『フィボナッチ数列』。
今のみなさんならフィボナッチ数列の一般項を導出することができます。
つまり、この漸化式を解くということ。
\(a_1=1, a_2, a_{n+2}=a_{n+1}+a_n\) によって定められる数列 \(\{a_n\}\) の一般項を求めよ。
興味ある人はぜひ解いてみてくださいね。
解説はこちらの記事から。
まとめ
いかがだったでしょうか?
三項間漸化式はちょっと計算量が多くて大変ですが、やることが決まっているので、慣れたらラッキー問題です。
漸化式のパズルみたいで面白い要素がギュッと詰まっています。
忘れた頃にもう一度この記事に戻って、復習してくださいね。
それではっ!
(当サイトでは、アフィリエイト広告を利用しています)


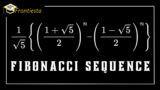




コメント