
こんにちは。

高校生のDaddyです。
今回は、ベクトルの超超超超キホン的なことを解説していきます。
『ベクトルは慣れだ!』という人もいますが、慣れるまでがとても辛い単元でもあります。
だって、わけわかんない文字が多すぎるんだもん!
ということで、ベクトルが極めて合理的な道具であるということを、一歩一歩丁寧に説明していきます。
教科書の何倍も噛み砕いて説明するので、その分記事が長め。
最後までついてきてください!
本記事は、『ベクトルとは何か』を体験的に理解できるようにすることを目的としています。ベクトルの厳密な定義や、具体的な計算方法を扱う記事ではございませんので、別記事をご参照ください。
『ベクトル』とは、矢印。

まずは、ベクトルという言葉の広さを感じてみましょう。
ベクトルとは、矢印のことです。
はい。まずはここまで理解してください。

いきなり、数学でなんで矢印なんか使うんだよ。

それはその通りや。本来、ベクトルは物理で大活躍するものやねん。
そもそも、数学は物理との相性が抜群です。
物理は数学を使ってこの世の事象を理解する学問です。
一方、数学はその計算技術を独自に発展させる学問と言えます。(ざっくりと説明しています)
物理でもっとも根本になるのは、チカラ。
どの方向で、どれくらいの強さでチカラを加えるかによって、モノの動きが変わります。
物理では、こういったチカラを『矢印』で書き表します。
この矢印をこれから、ベクトルと呼ぶことにしましょう。
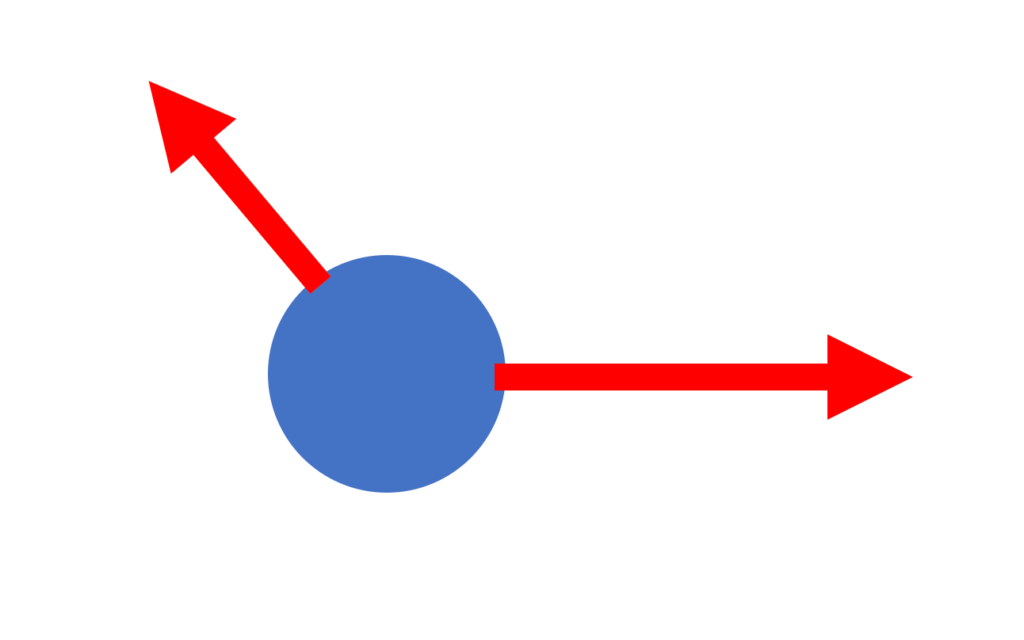
矢印の方向がチカラの方向で、長ければ長いほど大きなチカラになります。
矢印の大きさや向きを求める計算方法を編み出すのが、数学の役目。
私たちはこれからベクトルという単元を通して『矢印の計算方法』を学んでいくことになります。

え?矢印に足し算とか引き算とかがあるってこと?

その通りやな。ただ、ベクトルの扱いにはちょっと気いつけなあかんねん。
ベクトルは、普通の数ではない
ここで、勘違いしがちなことを挙げておきます。
それは、『ベクトルは普通の数じゃない』ということです。
ここでポイントになるのは、ベクトルは『向きを持つ』ということです。
ちょっとした具体例で考えてみましょう。
みなさんは、数字の大きさを比べることができます。

0と2、どっちが大きい?

そりゃ2でしょ。当たり前じゃん。
これは、数直線をかけば一目でわかります。
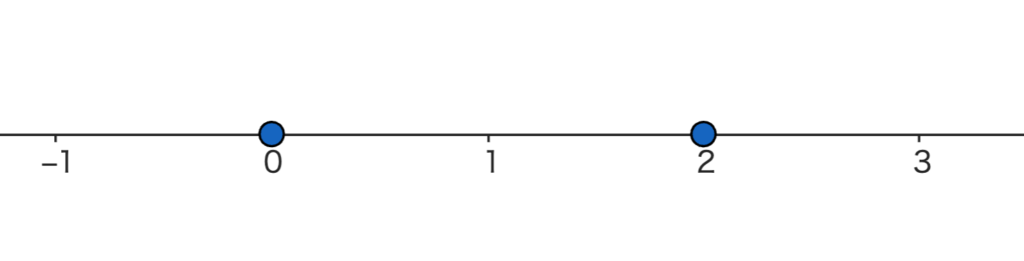
2つを比べて、より右にあるのが大きい数ですよね。
私たちは、数直線の上にある数ならどんな数でも、大きさを比べることができます。
でも、ベクトルではそうはいきません。
次のベクトル(矢印)は、どっちが『大きい』でしょうか?
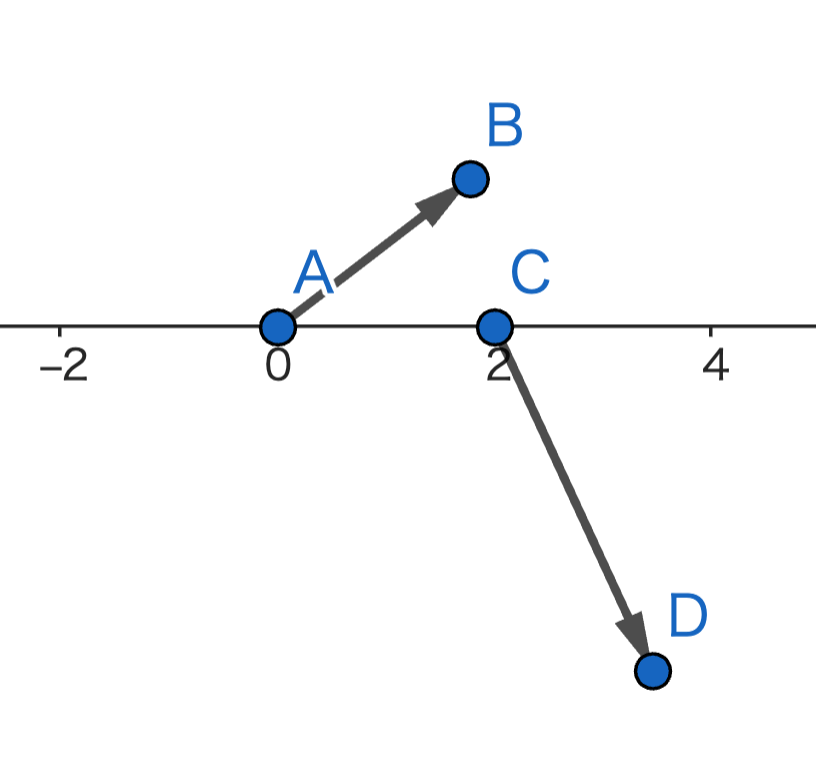

俺、怒るよ?数直線上にないじゃん。強いていうならCDの方が長いだろうけど。

『長さ』なんか聞いてへんで。どっちが『大きい』かを聞いてんねん。

比べようがないじゃん。だって数じゃなくて矢印なんだよ?
Zuttiくん、大正解です。
ベクトルには『向き』が必ず含まれています。
そのため、どっちが大きいかを比べること自体が間違っています。
一方で、ベクトルの長さを比べることはできますよね。
ベクトルから向きをなくせばただの長さになるからです。
このように、ベクトルはこれまでにない新しい概念として受け入れなくてはならず、計算のルールを決めるのも難しそうだということがわかります。
ちなみに、向きを持たない『普通の数』のことをスカラーと呼びます。ベクトルの対義語です。
ベクトルの書き表し方
さて、いよいよ数学っぽいことをやってきますよ!
まずベクトルは、矢印の始まりと終わりを決める必要があります。
先ほど使った画像をもう一度お見せしますね。

例えば、AからBに向かう矢印、みたいな感じです。
こういったベクトルを、これからは \(\overrightarrow{AB}\) と表すことにします。
なんかカッコイイですね。
読み方は、私の持っている教科書によると「ベクトルAB」。
一方で、かなり多くの数学の先生は「ABベクトル」と呼んでいます。
どちらでも正しそうです。
というかそんなの気にしない方がいいです。
さて、ベクトル同士は大きさを比べられないという話をしましたね。
ただ、長さを比べることはできます。
\(\overrightarrow{AB}\) の長さをどう表しましょう?
今後は、\(|\overrightarrow{AB}| = 3\) のように、絶対値記号をつけて表すことにします。

なんで絶対値の記号を使うの?プラスマイナスを入れ替えるわけじゃないのに。

それは絶対値の本質がわかってないな。
そもそも絶対値記号は、プラスマイナスを反転させる記号ではありません。
『距離』を表す記号です。
\(|-5|\) の答えが \(5\) になるのは、0から-5までの距離が5だからです。
これに当てはめて考えれば、\(|\overrightarrow{AB}|\) はAからBまでの距離を表していることがわかります。
向きを無視した、長さだけのスカラーに変化するのですね。
これは、複素数平面という分野でも活躍する考え方なので、よく理解してください。
なぜベクトルを学ぶのか
突然ですが、なぜベクトルを勉強するのでしょうか?
これは、図形問題を数式的に解くことができるようにするためです。
ベクトルを勉強すれば、ある意味『式変形』だけで図形問題が解けるようになります。
皆さんの中には、図形問題が苦手だという人もいるでしょう。
図形問題では、補助線を引いたり、相似な図形を探さなくてはならなかったりと、算数的なセンスが求められましたよね。
特に立体図形では空間把握が難しく、挫折した人も多いと思います。
しかし、ベクトルではその悩みをほぼ全て解決してくれます。
次の例題を見てみましょう。
平行四辺形\(ABCD\) について考える。線分\(AB\) の中点を点\(P\)、線分\(BC\) を \(3:2\) に内分する点を点\(Q\)、線分\(CD\) を \(2:1\) に内分する点を点\(R\)、線分\(CP\)と線分\(QR\)の交点を点\(S\)とする。この時、\(CS:SP\) を求めよ。
これ、かなり複雑ですよね。
まずは図を作ってから、線分を延長して相似比を求めて…みたいなことをしなくてはなりません。
ところがベクトルを使うと、次のようにエレガントに解くことができます。
(タップすると開きます)
点\(A\)を始点とした位置ベクトルを、\(\overrightarrow{b}=\overrightarrow{AB}, \overrightarrow{d}=\overrightarrow{AD}\)のように定める。
このとき、\(\overrightarrow{b}, \overrightarrow{d}\) は一次独立である。…(1)
内分点の公式から、
\begin{eqnarray}
\overrightarrow{AP} &=& \dfrac{1}{2}\overrightarrow{b} \nonumber\\
\overrightarrow{AQ} &=& \overrightarrow{b} + \dfrac{3}{5}\overrightarrow{d} \nonumber\\
\overrightarrow{AR} &=& \dfrac{1}{3}\overrightarrow{b} + \overrightarrow{d} \nonumber\\
\end{eqnarray}
また、\(\overrightarrow{AC} = \overrightarrow{b} + \overrightarrow{d}\)
ここで、\(S\)が\(PC\)上にあることから、実数\(s\)を用いて
\begin{eqnarray}
\overrightarrow{AS} &=& s \overrightarrow{AP} + (1-s)\overrightarrow{AC}\nonumber\\
&=& s \cdot \dfrac{1}{2}\overrightarrow{b} + (1-s)(\overrightarrow{b} + \overrightarrow{d})\nonumber\\
&=& (1- \dfrac{1}{2}s)\overrightarrow{b} +(1-s)\overrightarrow{d} \nonumber\\
\end{eqnarray}
同様にして、\(S\)が\(QR\)上にあることから、実数\(t\)を用いて
\begin{eqnarray}
\overrightarrow{AS} &=& t \overrightarrow{AQ} + (1-t)\overrightarrow{AR}\nonumber\\
&=& t (\overrightarrow{b} + \dfrac{3}{5}\overrightarrow{d}) + (1-t)(\dfrac{1}{3}\overrightarrow{b} + \overrightarrow{d})\nonumber\\
&=& \dfrac{1}{3}(1+2t)\overrightarrow{b} +(1-\dfrac{2}{5}t)\overrightarrow{d} \nonumber\\
\end{eqnarray}
(1)より、
\begin{eqnarray}
\left\{
\begin{array}{l}
1- \dfrac{1}{2}s = \dfrac{1}{3}(1+2t) \\
1-s = 1-\dfrac{2}{5}t
\end{array}
\right.\notag
\end{eqnarray}
\(\therefore (s,t) = \left(\dfrac{4}{13}, \dfrac{10}{13} \right)\)
したがって、\(CS:SP = s:(1-s) = \color{red}{4:9}\)
おそらく何をやっているかわからないでしょう。
しかし、式変形だけを変形だけを使って解けていることはわかると思います。
これがベクトル習得の第一目標です。
次回、計算方法を学ぶ!
申し訳ございません!
思ってたより記事が長くなってしまいましたので、記事を前編と後編に分けることにしました。
次回は、ベクトルの足し算と引き算、そして内積(掛け算みたいなやつ)を学習しましょう。
位置ベクトル・単位ベクトルの解説も次回行います。
まもなく記事を更新するので、ぜひご覧ください!
それではっ!



コメント