
こんにちは。Daddyです。
今回は、三平方の定理の逆というものを扱っていきます。
『逆』ってなんやねん、という人もいると思いますが、イチから徹底的に教えますので、ぜひ最後まで読んでください。
それでは、Let’s go!
逆とは
まず、逆がわからない人に解説します。(読み飛ばし可能)
数学において、『逆』という言葉には明確な定義があります。
命題「p⇒q」に対して、「q⇒p」を、元の命題の逆(ぎゃく、英: converse)と言う。
ある命題とその逆の真偽は、必ずとも一致しない(逆は必ずしも真ならず)。
Wikipedia より
……解説が必要ですね。
まず、『AならばB』という文章があったとき、数学ではAのことを仮定、Bのことを結論と呼びます。
ここまでは、日常生活で使う単語のレベルなので大丈夫でしょう。
次の文章を例に挙げます。(仮定ならば結論という配色です)
- 私がニューヨークにいるならば私はアメリカにいることになる
- この数が9の倍数であるならばその数は3の倍数である
- 今日が1600年ならばあなたはちょんまげをしている
ここで大事なのは、この仮定と結論の関係は、正しいとは限らないということ。(実際に、3つ目の文章は正しいとは限りません)
出題される時は、この問題が『正しいかどうか』を聞いてくるためです。
とにかく、『AならばB』という文章構造に対して、仮定と結論という名前をつけたというだけなのです。
そして、逆とは仮定と結論を入れ替えたものを言います。
次のような感じ。
- 私がアメリカにいるならば私はニューヨークにいる
- この数が3の倍数であるならばその数は9の倍数である
- あなたがちょんまげをしているならば今日は1600年
逆にした途端、文章が成り立たなくなってしまいました。
これは非常に大事な性質であり、逆は成り立つことも成り立たないこともあるのです。
今のとこ、成り立ってる例がないやん!と思っているかもしれませんが、結論から言うと、三平方の定理の逆は成り立ちます。
次のセクションに行きましょう。
三平方の定理の逆
いよいよここからが本番。
三平方の定理の逆を考えるには、もとの『三平方の定理』の仮定と結論を見抜かなければなりません。
復習はこちらから。
簡単にいえば、『その図形が直角三角形であるならば\(a^2+b^2=c^2\) である』というのが三平方の定理ですね。
なんと、三平方の定理に関しては、その逆である『\(a^2+b^2=c^2\)であるならばその図形は直角三角形である』も正しいというのです。
証明は後にして、問題を解いてみましょう。
次の三角形のうち、直角三角形であるものを選べ。
(1) 辺の長さが5cm, 12cm, 13cmの三角形
(2) 辺の長さが3cm, 4cm, 6cmの三角形
(3) 辺の長さが5m, 8m, 10mの三角形
三平方の定理の逆を使って解けば、この図形が直角三角形であるかどうか判定できます。
使い方はこんな感じ。
いずれも三平方の定理の逆を用いる。答えは(1)
(1)$$5^2+12^2=13^2(=169)$$三平方の定理が成り立っているので、この三角形は直角三角形である。
(2)
\begin{eqnarray}
3^2+4^2=25\nonumber\\
6^2=36\nonumber
\end{eqnarray}
したがって、\(3^2+4^2 \lt 6^2\) より三平方の定理は成り立たず、この三角形は直角三角形でない。
ちなみに、\(a^2+b^2 \lt c^2\) のような不等号の向きであるとき、この三角形は鈍角三角形である。
(3)
\begin{eqnarray}
5^2+8^2=89\nonumber\\
9^2=81\nonumber
\end{eqnarray}
したがって、\(5^2+8^2 \gt 9^2\) より三平方の定理は成り立たず、この三角形は直角三角形でない。
ちなみに、\(a^2+b^2 \gt c^2\) のような不等号の向きであるとき、この三角形は鋭角三角形である。
このように、三平方の定理が成り立つものだけが直角三角形になります。
ちなみに、上の解説では『直角三角形かどうか』だけでなく、『鋭角三角形か』『鈍角三角形か』にも言及しています。
これは、高校数学『余弦定理』から証明されるもので、今覚えるべきものではありませんが、興味があればぜひ調べてください。
証明
証明は教科書に必ず載っているものですが、文字だらけで非常にわかりづらいです。そこで今回は、噛み砕いた表現で証明します。
論理的なミスはありませんが、表現がやや数学的でないのはご了承ください。
まず、何を証明するのかを確認します。
『\(a^2+b^2=c^2\)であるならばその図形は直角三角形である』を証明するのでした。
まずは、仮定に合う図形を用意しましょう。
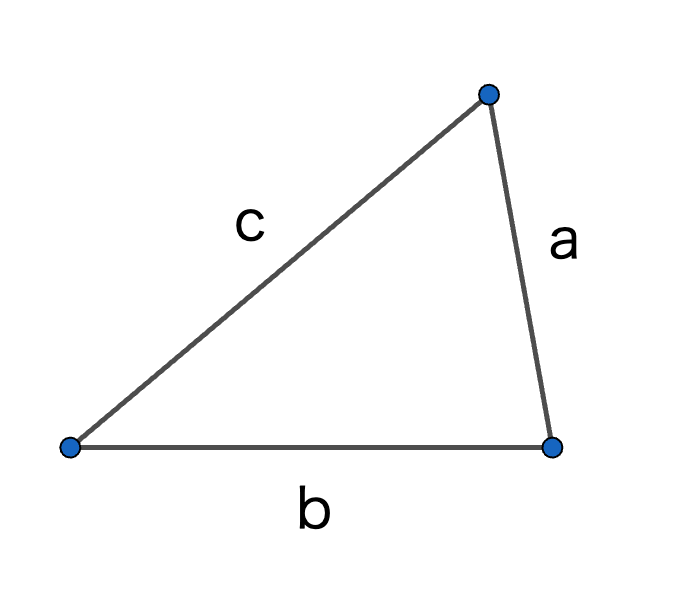
これは、直角三角形かどうかはわからないけど \(a^2+b^2=c^2\) は成立する三角形です。
これが直角三角形であると証明できれば、『\(a^2+b^2=c^2\)であるならばその図形は直角三角形である』を証明したことになります。
次に、上の三角形の2辺 \(a, b\) は同じ長さで、その間の角が直角であるような三角形を用意します。
斜辺の長さは今のところ \(c\) ではないので、とりあえず \(x\) としましょう。
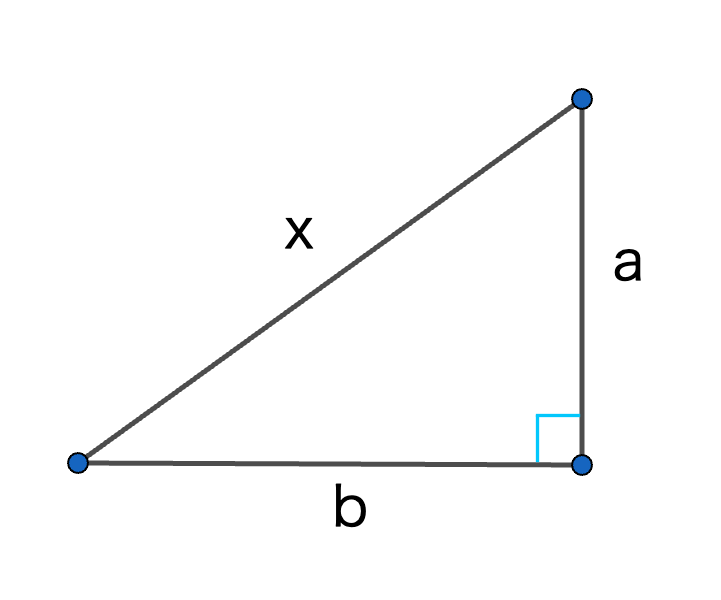
この三角形は直角三角形なので、三平方の定理が使えますから、\(a^2+b^2=x^2\) となります。(ココ大事)
ここで思い出しましょう。
1つ目では、直角三角形かどうかはわからないけど \(a^2+b^2=c^2\) は成立する三角形を用意しました。
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2=c^2 \\
a^2+b^2=x^2
\end{array}
\right.\notag
\end{eqnarray}
これを連立させると、\(c^2=x^2\) となっていることに気づきますね。
\(c, x\) ともにマイナスになることはありませんから、\(c=x\) が成り立ちます。
ここで、2つの三角形は、3辺の長さがすべて等しいから、合同であるといえます。
合同な三角形の対応する角は等しいから、1つ目の三角形も、\(a, b\) に挟まれた部分は直角になります。
よって、直角三角形かどうかはわからないけど \(a^2+b^2=c^2\) は成立する三角形は、結局直角三角形でした。
証明終了!
まとめ
いかがだったでしょうか?
三平方の定理の逆は、決して当たり前のように成立するものではなく、合同を用いてしっかり証明しなくてはならない内容です。
この性質は非常に重要であり、将来、高校数学で『必要十分条件』『余弦定理』などを勉強するときにそのまま生かされます。
しっかり復習して、身につけていきましょう。
それではっ!



コメント