
こんにちは。Frontiesta代表のDaddyです。
今回は、直角三角形の合同条件というものを中学2年生に向けて解説します。
結論からいうと、直角三角形の合同条件は『証明』することができます。
しかし、難しい問題を解くにあたって、合同条件をたくさん覚えておくことは、極めて重要。
速く、正確に解くことができるからです。
必ず、必ず、必ず暗唱してくださいね。
三角形の合同条件
ところで、三角形の合同条件といえば、次の3つですね。
- 3組の辺がすべて等しい(三辺相等)
- 2組の辺とその間の角がそれぞれ等しい(二辺夾角相等)
- 1組の辺とその両端の角がそれぞれ等しい(二角夾辺相等)
この3つは、直角三角形の合同条件を覚えるよりもずっと大事です。
わからなかった人は下のリンクでリンクで要復習!
直角三角形の合同条件を証明するときに使うので、よく覚えておきましょう。
直角三角形の合同条件
さて、いよいよ本題。
直角三角形の合同条件は、次の2つになります。
- 斜辺と1つの鋭角がそれぞれ等しい
- 斜辺と他の1辺がそれぞれ等しい
『いや、覚えられるかいっ!』ていうのは数学では『あるある』ですよね。
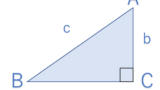
まず、両方の合同条件に入っている斜辺というワードから確認しましょう。
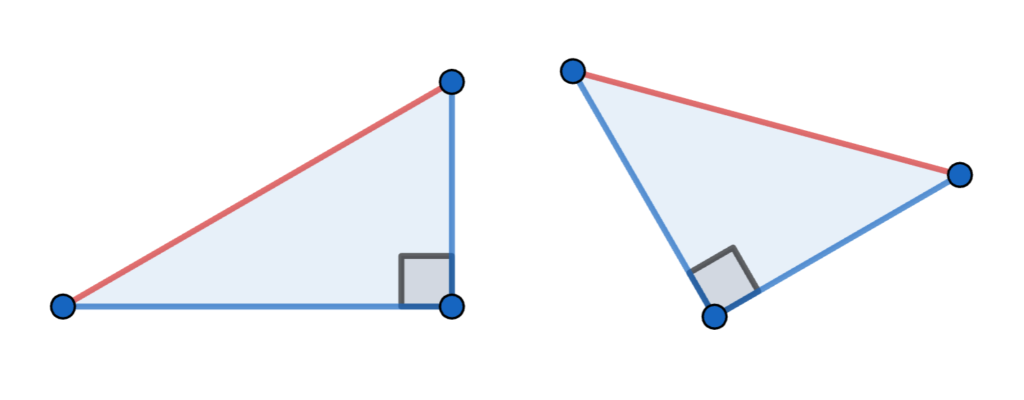
斜辺は、上の図で赤線で示されている、直角の反対側にある辺のことです。
直角三角形の合同条件では、斜辺が等しいかどうかというフレーズが必ず入っています。
その上で、あと一つの条件を満たしていれば、合同だということができるのです!
その条件とは、次の2つの条件のどちらかです。
- 1つの角が等しい(ただし直角以外!)
- 1辺が等しい(ただし斜辺以外!)
こうやってみれば、少しわかりやすくなったでしょうか?
証明してみよう
さて、なぜこの2つの合同条件が成り立つのか、気になりますよね。
ということで、証明してみましょうか。
証明問題の解き方を覚える良いきっかけになるので、ぜひ解答をノートに『写して』みてください。
(1) 斜辺と1つの鋭角がそれぞれ等しい2つの直角三角形は合同であることを証明する。
下の図は、その条件を三角形にしたものである。(赤い部分が等しい)
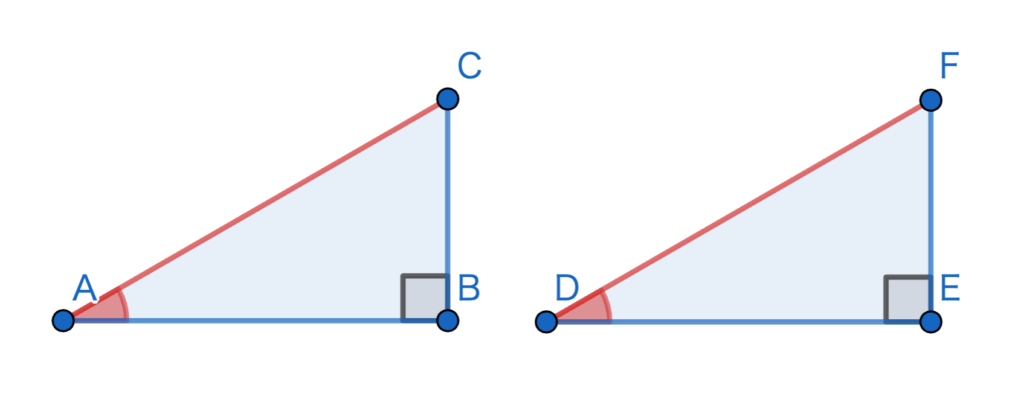
仮定より、\(\angle B = \angle E\) …(1)
仮定より、\(AC=DF\) …(2)
仮定より、\(\angle A = \angle D\) …(3)
ここで、三角形の内角の和は \(180^{\circ}\) だから
\(\angle C = 180^{\circ}-\angle A-\angle B\)
\(\angle F = 180^{\circ}-\angle D -\angle E\)
(1)(3)より \(\angle C = \angle F\) …(4)
(2)(3)(4)より、1組の辺とその両端の角がそれぞれ等しいから、\(\triangle ABC \equiv \triangle DEF\)
(2) 斜辺と他の1辺がそれぞれ等しい2つの直角三角形は合同であることを証明する。
下の図は、その条件を三角形にしたものである。(赤い部分が等しい)
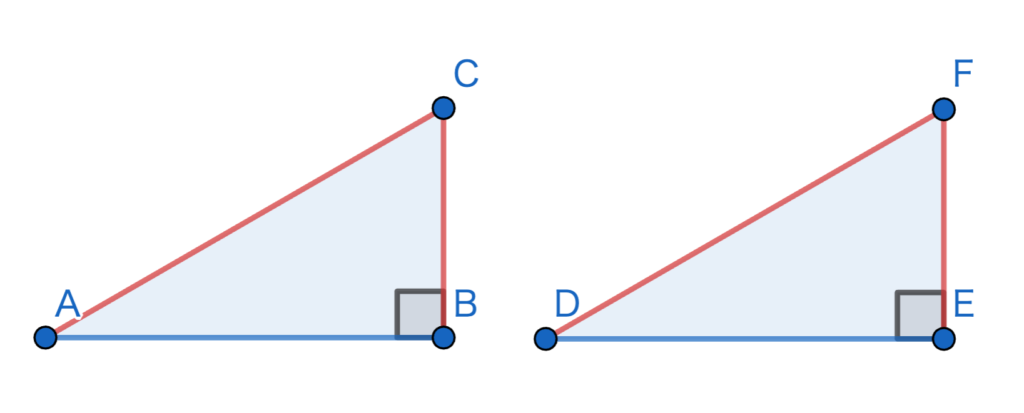
ここで、\(BC=EF\) …(1) であり、\(\angle B + \angle E = 180^{\circ}\)から2つの三角形をつなぎ合わせると三角形を作ることができる。
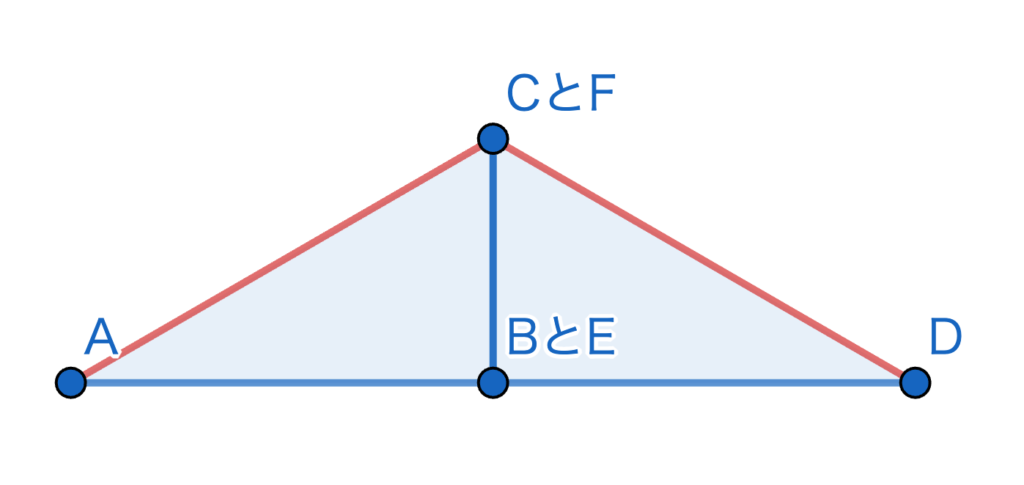
仮定より、\(AC=DF\) …(2) だから、この三角形は二等辺三角形である。
二等辺三角形の頂角の二等分線は、底辺を垂直に2等分するから、\(AD=DE\) …(3)
(1)(2)(3)より、3組の辺が全て等しいから、\(\triangle ABC \equiv \triangle DEF\)
ちなみに、三平方の定理を使うと、式だけでカンタンに \(AB=DE\) を証明することもできます。下にリンクを貼っておくので、その理由を考察してみてください。
証明方法はこれ以外にもいくつかあります。
教科書に載っている証明方法とは異なると思うので、研究してみてくださいね。
まとめ
いかがだったでしょうか?
教科書や参考書ではサラッと軽く扱われているだけなので、独学で理解するにはやや難しい分野だと思います。
ぜひこの記事を読み返して、理解を完全なものにしてください。
最終的な目標は『暗唱すること』ですよ!
おすすめの問題集は最後にまとめておきますので、気になったものがあればカートに入れてみてください。
個人的には『受験研究社』の参考書が取り組みやすくておすすめ。
コロナの休校期間で愛用していました。
それではっ!




コメント