『三角形の合同条件』を現役高校生がわかりやすく解説！【中2数学】

こんにちは。フロンティエスタ代表のDaddyです。

今回は、三角形の合同条件というものを扱います。

この分野は数学としては珍しい暗記ゲーです。

とにかく『3つの合同条件を覚える』ことにこだわりましょう。

それでは、Let’s go!

なぜ合同条件を覚えるのか？

結論から言うと、難しい図形の問題を解いたぜ！ということを証明するときに、『なぜ君は正しいと思うのか』という根拠を用意しておくためです。

数学者たちは言語や文化の壁を超えて、誰もが納得のいく証明を求めています。

例えば、

という問題に対して、頭の良い人が

と言ったとしましょう。

その理由を頭の良い人に聞くことには、

……納得いかない。

この原因は、『根拠』が意味不明で、論理に飛躍があるからです。（完全に間違っているわけではないけど）

証明するためには、みんなが納得のいくルールというものを決めて、それらを駆使していく必要がある、ということがよくわかります。

というわけで、三角形の合同条件を覚えて、図形に関する証明問題をしっかり解けるようになっていきましょう。

究極な話、全ての図形は切り刻みまくれば三角形だけにすることができるので、三角形の合同条件は非常に重要なのです。

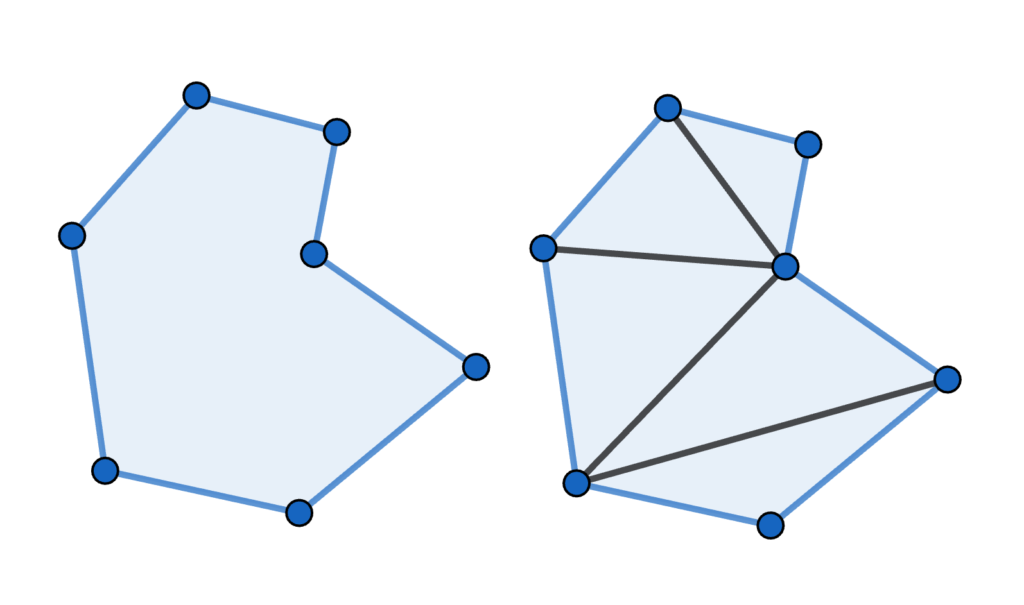
小学生の復習：作図

小学生の頃、三角形や平行四辺形をコンパスと定規で作図していたと思います。

ここで三角形について質問。

作図の問題で与えられた条件はいくつだったでしょうか？

正解は『3つ』。

このようなテストを解いた記憶、残っているのでは？

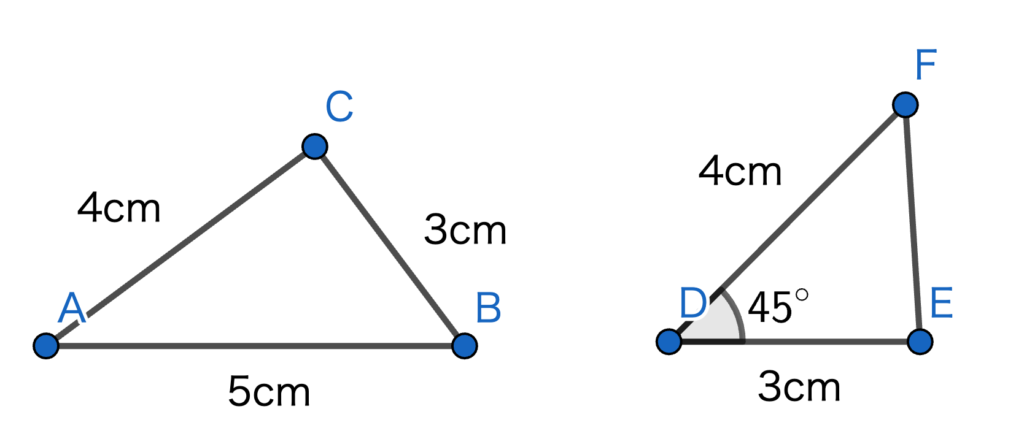
ここからわかるように、辺の長さや角の大きさなど、一つの三角形には必ず3つの条件が書き込まれています。

例えば、1つ目の三角形では辺の長さの条件が3つ与えられていて、2つ目の三角形では辺の長さの条件が2つ、角の大きさの条件が1つで、合わせて3つ与えられています。

こうした作図するための3つの条件には、とある規則があり、頭の良い人たちがこの規則を合同条件として分類しました。

こうした合同条件を根拠にこれらをうまく組み合わせることで、複雑な図形についての証明問題を解いていくわけです。

三角形の合同条件

三角形が合同であるためには、3つの条件がそろえば良いと言いましたが、3つの条件があればなんでも良いというわけではありません。

例えば、3つの角が全て等しい、と条件が与えられていても、合同であるとは限りません。

三角定規は、どんなものでも角が等しいですが、大きさはそれぞれ異なります。

このように、必ず合同になる条件というものを調べていくと、たった3つに分類することができます。

3組の辺がすべて等しい

要するに、全部の辺が等しければ、三角形においては必ず合同だということ。

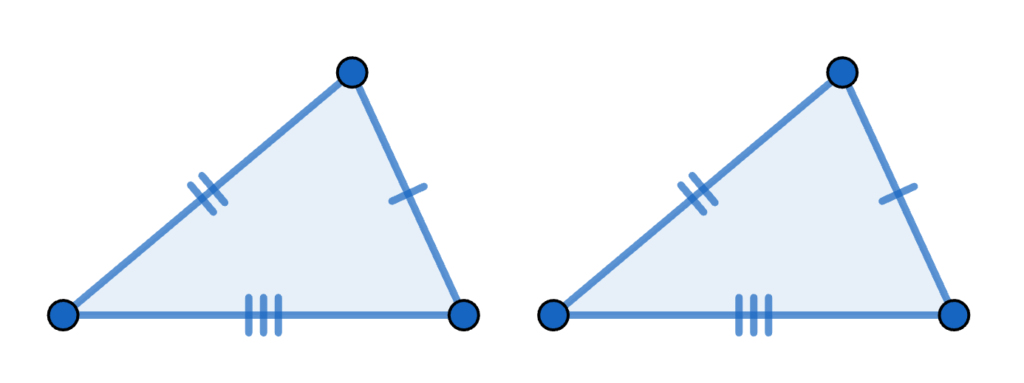
例えば、辺の長さが3cm, 4cm, 5cmの三角形をかいてくださいっていうと、全員が同じ図形をかくことができるということです。

図形の向きは、合同を考える上では気にする必要はありません。

この合同条件をカッコよく言いたければ、『三辺相当』なんて表現もあります。

2組の辺とその間の角がそれぞれ等しい

ここからが少し覚えづらいですね。

下の図形を見ましょう。

まず、2組の辺が等しいのが最低限クリアするべき条件です。

あとはどこか1組の角が等しければ良さそう。

結論からいうと、2つの辺に挟まれた角が等しければ確実に合同です。

実際に、辺の長さが4cm, 5cmで、その間の角が45度である三角形は1通りしか作ることができません。

ちなみに他の場所にある角が等しくても、合同にならない場合があります。（後述）

1組の辺とその両端の角がそれぞれ等しい

これがなかなかに厄介。

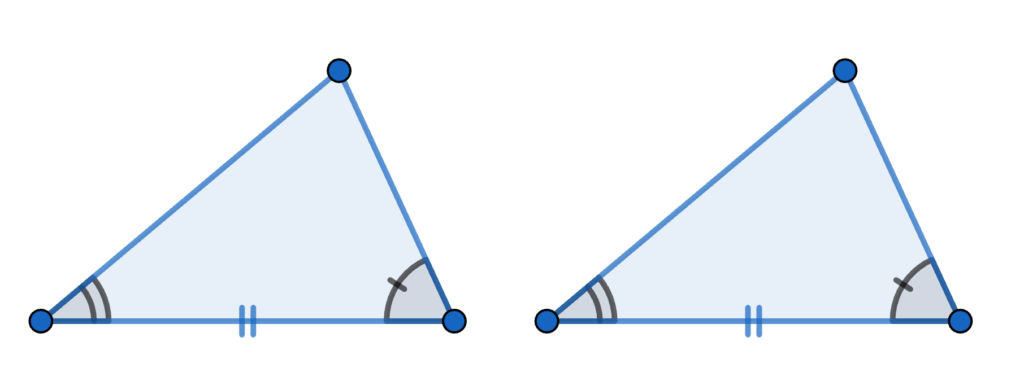
この合同条件の意味を説明すると、まず2組の角が等しいことが大前提です。

そして、間に挟まれている辺が等しければ合同であるということ。

ところが、実際に暗唱しなければならないのは『1組の辺とその両端の角がそれぞれ等しい』という条件なんですよね。

言ってることは一緒なのですが、やや理解しづらい。

頑張るしかありません。

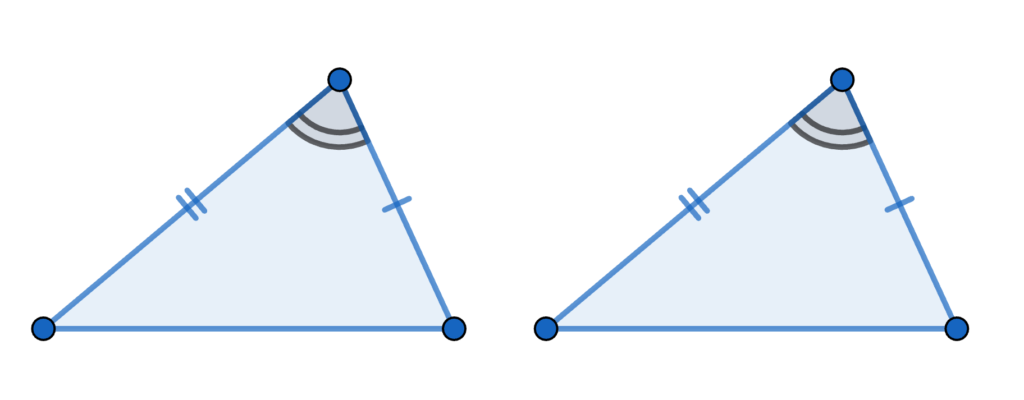
まちがった合同条件に注意

先ほど忠告したように、3つの条件があればなんでも良いというわけではありません。

例えば、下の図形は『2組の辺と1組の角が等しい』という条件で作図した三角形です。

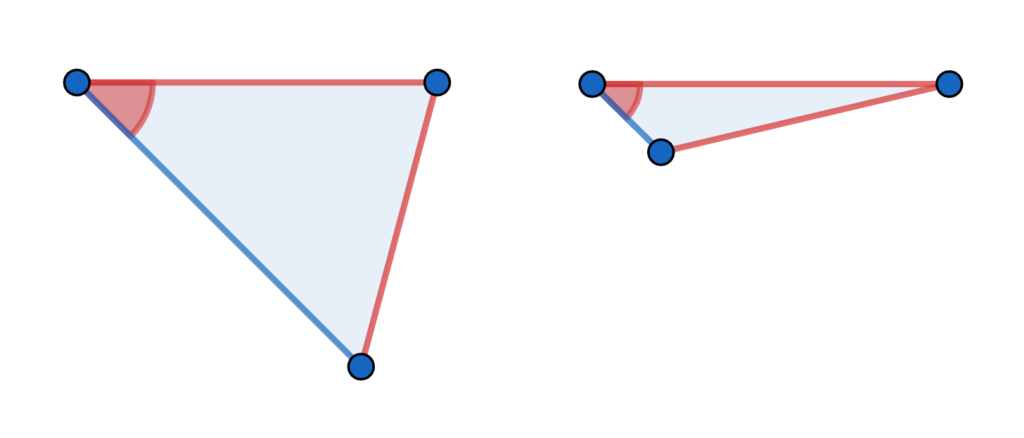
これは合同でしょうか？

違いますね。

『2組の辺とその間の角が等しい』というように、等しい角の場所を決めないと、このような間違いが発生してしまいます。

合同条件は3つより多いことも少ないこともありませんから、間違えないようにしましょう。

合同条件の覚え方

丸ごと暗唱する

とにかくこれが基本中のキホン。

声に出して覚えるのがおすすめです。

暗記の精度が70%くらいになったら問題演習に取りかかり、証明してつかっていく中で丸ごと暗唱してきましょう。

規則性で覚える

三角形の合同条件は、与えられる条件が必ず3つなので、等しい辺と角の数には規則性があります。

そのため、表を作ると覚えやすいかもしれません。

等しい辺の数	等しい角の数
3	0
2	1
1	2

ただ、注意すべきこともあります。

1つ目は、等しいものの位置がわからないということ。

先述したように、合同条件には『2組の辺と1組の角が等しい』というものはありませんが、上の表ではその違いがわかりません。

辺と角の位置関係は別に覚えておく必要があります。

2つ目は、『3組の角がそれぞれ等しい』という合同条件が存在しないということ。

表を作るときは、『合同条件は3種類しかない』ということを念頭に作っていくべきです。

このように、規則性で覚えるのはやや危険なので、あくまで補助として活用しましょう。

まとめ

それではここで画面をスクロールするのを止めて、一度暗唱してみましょう。

答えは下に用意しています。タップすると答えを見ることができます。

とにかく暗記ゲーですから、何度も声に出して覚えましょう。

なお、表記は教科書によって微妙に異なるので、学校で暗唱テストなどがあるようであれば、そちらの表記で覚えてください。

それではっ！