
こんにちは。現役高校生のDaddyです。
今回は、重複組合せ \(H\) について解説します。
最上位クラスの子であれば、中学受験で学習することもある単元です。
一応、\(H\) という文字を使った公式はありますが、何より原理を知ることが大切です。
公式暗記より、解答に持っていくまでの流れを身につけていきましょう。
それでは、Let’s go!
重複組合せとは
重複組合せって何でしょう?
今回の単元では、名前を覚えることよりも、実際に問題が解けることの方がよっぽど重要なので、先に例題を解いてイメージをつけましょう。
りんご、みかん、いちご、バナナがたくさんある。この4種類のくだものの中から6つ選びたい。このとき、くだものの選び方は何通りか。ただし、選ばないくだものがあっても良い。
例)りんご3つ、いちご2つ、バナナ1つ
ふつうの組合せの問題とは少しだけ違うところがありますね。
ふつうの組合せの問題では、4種類のくだものが1つずつあって、その中のいくつかを選ぶ形式でした。
ところが今回は、4種類のくだものがたくさんあって、選ぶ種類がかぶっても良いからとにかく選ぶ形式です。
ふつうの組合せを忘れた人は、下の記事でぜひ復習してください。
この問題は、\({}_4 \mathrm{C}_6\) とするわけにもいきませんし、テキトーに \(4^6\) としてしまうのも良くありません。
この解答を思いつくのは難しいので、一つのパターンとして身につけておいてください。
文章が長いですが、じっくり読むこと。
- Step1いきなり丸と棒を用意する

選ぶくだものは6こなので、6こ丸を用意する。
果物の種類は4種類なので、そこから1つ引き算した3つの棒を用意する。
なぜか?という疑問はとりあえず無視する。 - ラベル並べ替えてみる
丸と棒を試しに並べ替えてみる。
下はその一例。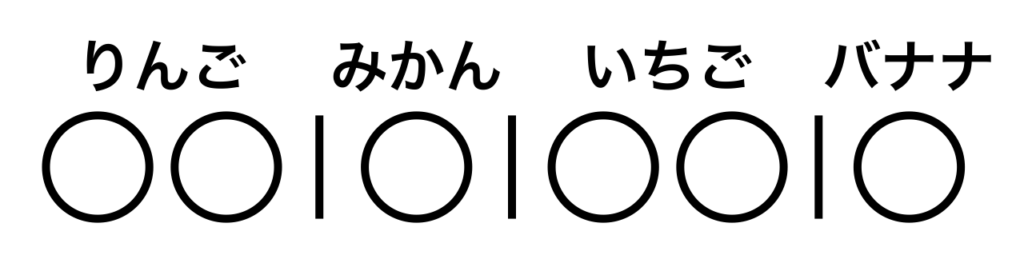
棒を仕切りと見立てて、左から順にりんご、みかん、いちご、バナナとし、丸の個数がそれぞれの果物の選び方とすることができる。
今回の例では、りんご2こ、みかん1こ、いちご2こ、バナナ1こ。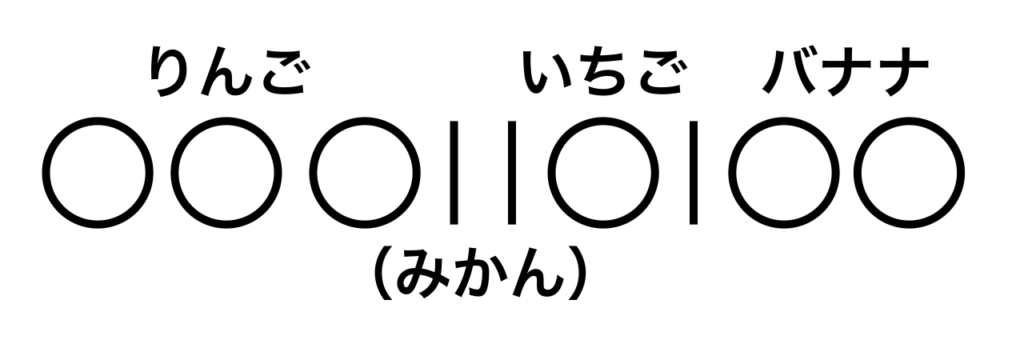
上のように、棒が連続すると、そのくだものは0個とみなすことができる。今回の例では、みかんが0こ。
- ラベル順列を求める
つまり、6つの丸と3つの棒を並べ替える、順列の問題であることがわかった。ひとまず9つのものがあるので、単純な順列は \(9!\) 通り。
\(9!\) は、\(9 \times 8 \times 7 \times \cdots \times 3 \times 2 \times 1\) を意味します。\(!\) は、その数をスタートに、1ずつ減らした数をかけ算していく記号です。
- ラベル重複をなくす
ただし、丸どうしは区別がないので、入れ替えると重複してしまう。6つの順列の分だけ重複しているので、\(6!\) で割ればよい。
同様に、棒どうしは区別がないので、入れ替えると重複してしまう。3つの順列の分だけ重複しているので、\(3!\) で割ればよい。
したがって、\(\dfrac{9!}{6!3!}=84\) より84通り
丸と棒を使って並べ替える問題でした。
このように、たくさんの種類のものがたくさんあって、何回選んでも良いし、1回も選ばないものがあっても良い時の組合せのことを、重複組合せといいます。
この発想は、本当に難しい…
中学受験生(ハイパー小学生)がこれを理解できるのが、本当にすごいです。
Hを使った表記
ところでこの計算、どうやら規則がありそうです。
さっきの計算も、一見大変そうで、結構綺麗に約分できましたよね。
先ほどの \(\dfrac{9!}{6!3!}\) で試してみましょう。
これをかけ算のカタチに変えると、\(\dfrac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(6 \times 5 \times 4 \times 3 \times 2 \times 1) \times (3 \times 2 \times 1)}\) となりますね。
ここで、分母にも分子にも \(3 \times 2 \times 1\) のカタチがありますから、約分できます。
したがって、\(\dfrac{9 \times 8 \times 7 \times 6 \times 5 \times 4}{6 \times 5 \times 4 \times 3 \times 2 \times 1}\) となります。

このカタチ、みたことあるで…!
そう、このカタチは \({}_{9} \mathrm{C}_{6}\)と完全に同じです。
今回の問題は、\({}_{9} \mathrm{C}_{6}\) の式さえ思いつけば、一発で求めることができました。
じゃあ、この9っていう数と、6っていう数はどこから生まれたものでしょうか?
9は丸と棒の数の合計、6は丸の数です。
ところで、丸の数は、選ぶくだものの個数で6こ、棒は、くだものの種類の個数-1で(4-1)こです。
したがって、\({}_{4+6-1} \mathrm{C}_{6}\) となるのです。
これをあらたに公式としたものが、\(\mathrm{H}\)。
これからは \({}_{4} \mathrm{H}_{6}\) のように、\(\mathrm{H}\) を使って、選ぶものの種類を左下に、選ぶ個数を右下に書くことにします。
\(\Box\) 種類のものがたくさんあり、重複して \(\bigcirc\) 個のものを選ぶとき、\({}_{\Box} \mathrm{H} _{\bigcirc}\) と表す。
計算方法は下の通り。
\({}_{\Box} \mathrm{H} _{\bigcirc} = {}_{\Box + \bigcirc -1} \mathrm{C} _{\bigcirc} = \dfrac{(\Box + \bigcirc -1)!}{\bigcirc ! (\Box -1)!}\)
とはいえ、全ての人がこの公式を覚えているわけではありません。
重複組合せでは、丸と棒を並べ替えるのだ、ということを覚えておけば、その場で公式を作ってしまうことができるからです。
覚えても良いし、覚えなくても良いということを『覚えて』おいてください。
組合せCとの違い
ここまできたみなさんならわかるはず。
\(\mathrm{C}\) と \(\mathrm{H}\) では性質が大きく異なりますね。
\(\mathrm{C}\) では、たくさんの種類のものから、1つずつとる組合せを求めます。
\(\mathrm{H}\) では、たくさんの種類のものがたくさんあって、何回選んでも良いし、1回も選ばないものがあっても良い時の組み合わせを求めます。
\(\mathrm{H}\) は、どちらかというと順列に近いような考え方をします。
まとめ
いかがだったでしょうか?
発想がなかなかに難しい \(\mathrm{H}\) ですが、一度その解法を身につけたら、その美しさに感動すること間違いなし。
明日もう一度だけ復習して、知識を定着させてください。
公式は覚えても良いし、覚えなくても良いんですよ!
それではっ!




コメント