
こんにちは。
数学大好きDaddyです。
今回は2次関数、特に解の配置条件を扱っていきます。
残念ながら、高校数学でイチバン最初につまづいてしまう単元は、この『2次関数』です。
でも、原因は単純明快。
ズバリ、正しくグラフを作れているかどうかで決まります。
問題演習をたくさんしていく中で、身につけていきましょう!
2次方程式を復習してみよう
この章は、解の配置条件を勉強するために必要な、2次方程式の復習になります。
数学が得意な方は、ざっと目を通して、次の章に進んでいただいて構いません。
平方完成
平方完成は、次のように2次方程式を変形することです。
例えば、こんな感じ。
\begin{eqnarray}
2x^2-8x+9&=&0\nonumber\\
\iff 2(x-2)^2+1&=&0\nonumber
\end{eqnarray}
\(ax^2+bx+c=0\) という至ってシンプルな2次方程式のカタチを、\(a(x-p)^2+q=0\) という2乗のカタチを無理やりつくったような感じですね。
めちゃくちゃ使う変形なので、覚えていない方は早速復習しておきしょう。
判別式
判別式は、2次方程式が解をもつかどうかを調べる式のことです。
2次方程式の解の公式を見てみましょうか。
下の式で、赤く色づけられているところが判別式です。
$$x=\dfrac{-b \pm \sqrt{\color{red}{b^2 -4ac}}}{2a}$$
ズバリ、ルートの中身です。
ルートの中身がマイナスになってはいけないのはご存知の通り。
マイナスになったら解なしですし、プラスになったら2つの解を持ちます。
0になったら、どうなるでしょうか?
$$x=\dfrac{-b \pm \sqrt{0}}{2a}=-\dfrac{b}{2a}$$
\(\pm\) が消えたことから、1つの解をもつことがわかりますね。
\(b^2-4ac\) のプラス、マイナス、0を判別すれば、解をいくつ持つのか調べられるのです。
解の配置条件とは?
解の配置条件は、いろんな呼び方があり、『解の存在範囲』という呼び方も一般的です。
結局、問題が解けたらどうでも良いのですけどねw
『解の配置条件』の問題といっても、いろいろあります。
今回は超王道の問題を見ていくことにしましょう。
例題を見てみよう
\(x\) についての2次方程式 \(x^2-2ax-2a+3=0\) は \(0 \leqq x \leqq 2\) で解を2つもつ。
このとき、 \(a\) の範囲を求めよ。
解き方、わかりますか?
超超超天才でない限り、初見で解くのは難しいでしょう。
なぜなら、とある3つの条件を組み合わせて解く必要があり、とても複雑だからです。
でもご安心を。
グラフを作れば理解できること間違いなし。
その辺は後で解説します。
ひとまず、\(f(x)=x^2-2ax-2a+3\) とおいて、以下は \(f(x)=0\) と2次方程式を省略しましょう。
式は短くてシンプルな方が見やすいのでね。

ほな、グラフ作ってこか。
ということで、\(f(x)\) を平方完成します。
\begin{eqnarray}
f(x)&=&x^2-2ax-2a+3\nonumber\\
&=&(x-a)^2-a^2-2a+3\nonumber
\end{eqnarray}
正しく平方完成できましたか?
そして、\(y=f(x)\) つまり \(y=(x-a)^2-a^2-2a+3\)(平方完成した後の式)のグラフについて考えていけば良さそうです。

\(y=(x-p)^2+q\) の軸は、どうやって表すか、覚えてるか?

確か、平方完成したカッコの中身、\(p\) を使うんだったよね。
\(x=p\) が軸かな?

合うてるで。
てことは、今回のグラフやと、軸は \(x=a\) やな。
それでは、グラフを作っていきましょう。
\(a\) の値が決まっていないので、問題文にあったグラフを、1つだけ作ればひとまずOK。
こんな感じですね。
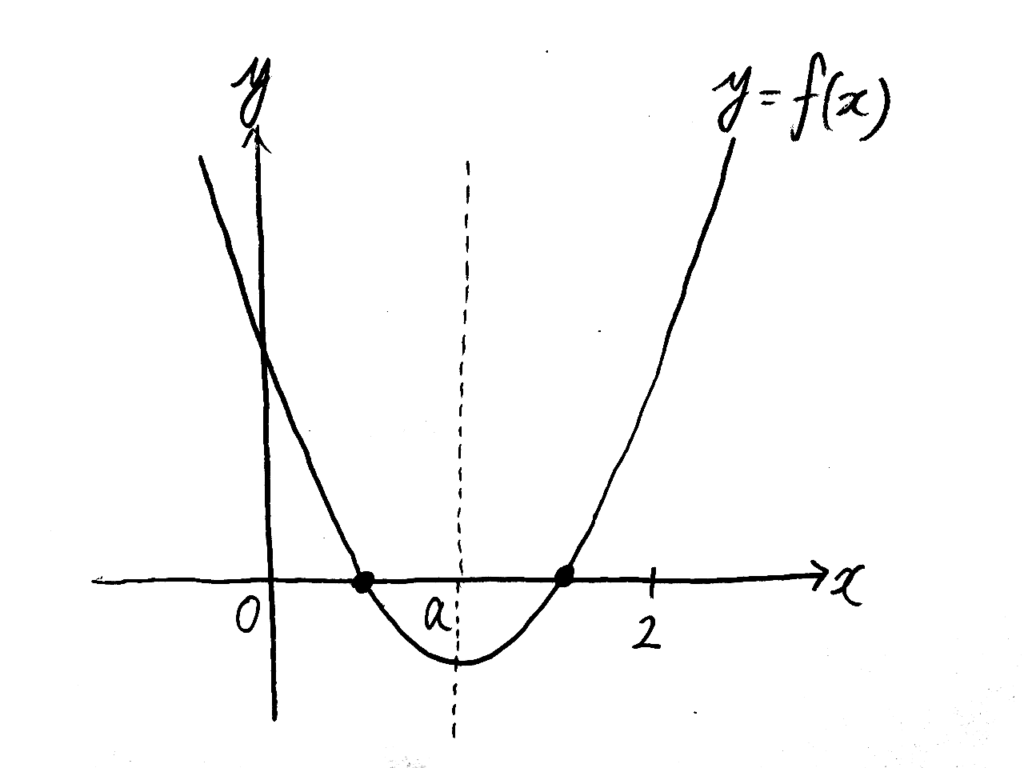
\(0 \leqq x \leqq 2\) で2解をもつ、というのが問題文の条件にありましたが、要するに、0と2の間で交点が2つあれば良いということですね。

え?なんでだっけ?

\(y=f(x)\) のグラフで、\(y=0\) になる時を考えんねん。
\(0=f(x)\) になって、これが2次方程式になってるやろ?

あとは、\(y=0\) っていうグラフを描くと、x軸そのものだったね。
交点を見ればいいのは、そういうことか!
あとは、このようなグラフを描くことができる \(a\) の範囲を求めれば良さそうですね。
それでは、次の3つの条件を考えてみましょう。
- 判別式
- 軸
- 端点
ゆっくり解説していくので、まだ覚えたりする必要はありません。
ここから長いですが、しっかりとついてきてください!
1つ目:判別式
問題文の条件から、\(f(x)=0\) という2次方程式が2つの解を持たなくてはならないんでしたよね。
2つの実数解を持つ、ということは…?

判別式が0より大きい!
間違ってはいないのですが、判別式が \(b^2-4ac\) と表されることはまずありません。
『\(a, b, c\) ってなんの数やねん』と突っ込まれてしまうからです。
そのため、ふつうは \(D\) を使って表します。
計算してみましょう!
\begin{eqnarray}
D&=&(-2a)^2-4\cdot1\cdot (-2a+3)\nonumber\\
&=&4a^2+8a-12\nonumber\\
&\gt&0\nonumber\\
\end{eqnarray}
\(a\) だけの式になったので、範囲が求められそうですよ!
この調子で不等式を解きましょう。
\begin{eqnarray}
4a^2+8a-12 &\gt& 0\nonumber\\
a^2+2a-3 &\gt& 0\nonumber\\
(a-1)(a+3) &\gt& 0\nonumber\\
\nonumber\\
\therefore \ a \lt -3, 1 \lt a \nonumber
\end{eqnarray}
この結果、どこかにメモしておいてください。
2つ目:軸

グラフ描いたとき、軸の位置はどの辺にあった?

そうだね…
大体だけど、0と2の間にあるかな。

そこがめっちゃ大事。
0や2の外側に軸があると、2つの解が0と2の間に入らなくなんねん。
そう。
軸の位置が実はめちゃくちゃ大事です。
今回の軸は \(a\) ですよね。
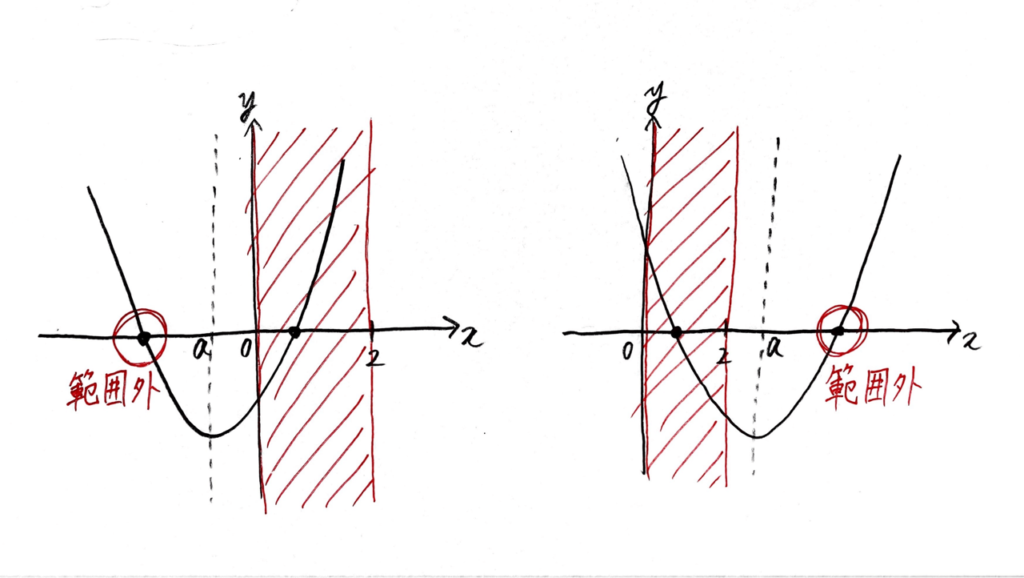
ということで、\(0 \lt a \lt 2\)
これもメモしておいてください。
3つ目:端点
最後に、端点を調べます。
端点というのは、\(x\) の範囲の端っこのこと。

今回は \(0 \leqq x \leqq 2\) なので、0と2のことやな。
なぜ端点を調べなくてはならないのか。
実は、1つ目の条件も、2つ目の条件も、どっちも満たしていても、まだ \(0 \leqq x \leqq 2\) で2つの解を持たない場合があります。
それが、次のような時。
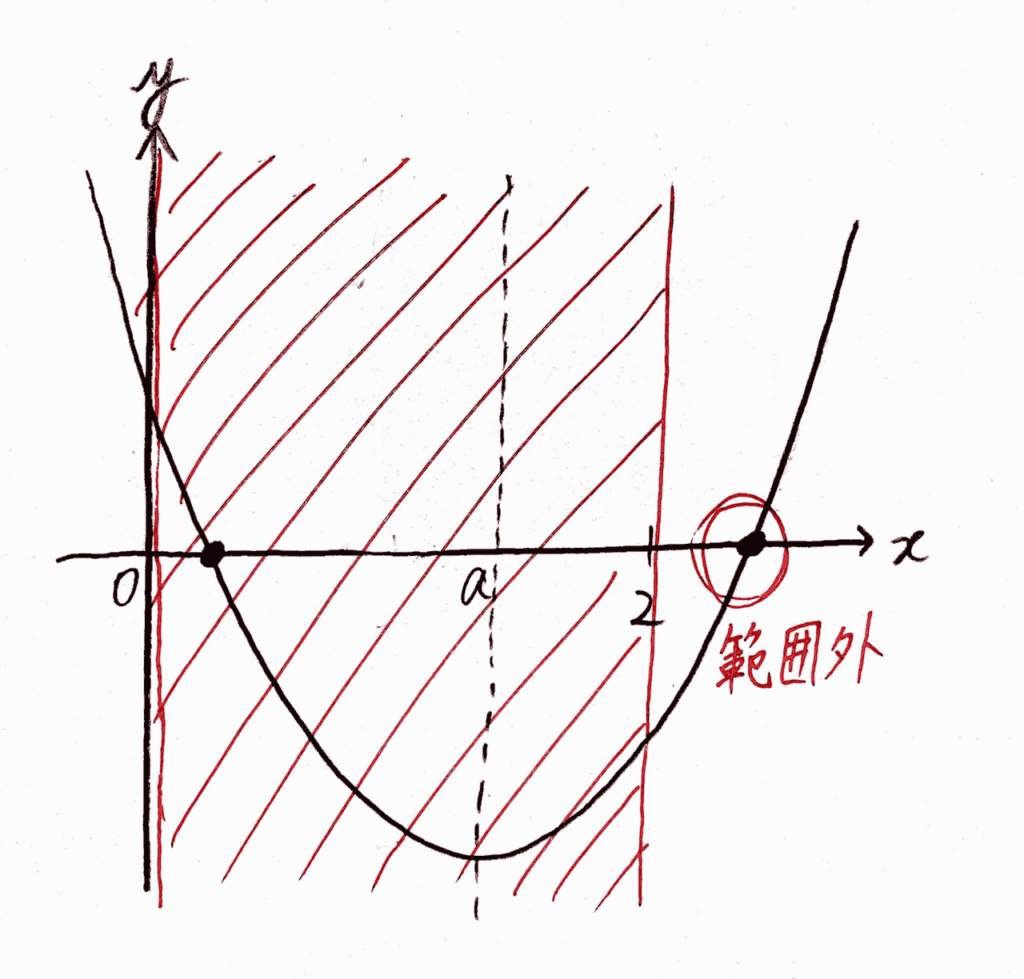

こんなの言いがかりだ!
このような例を自力で見つけるのは大変です。
ですが、解の配置条件では端点を調べるというふうに覚えておけば、次からは解けるようになります。
端点を調べる、というのは、次のようなこと。

\(f(0)\) も、\(f(2)\) も、どちらも0またはプラスなんですよね。(グラフでは0の場合をかけていませんが、ご了承ください)
必ずx軸上か、それより上側に位置しています。
これを数式にして、\(a\) について解きましょう。
\(x=0\) や \(x=2\) は、平方完成する前の式 \(f(x)=x^2-2ax-2a+3\) に代入すると計算がラクですよ。
\begin{eqnarray}
& \quad &
\left\{
\begin{array}{l}
f(0) \gt 0 \\
f(2) \gt 0
\end{array}
\right.\notag
\nonumber\\
\nonumber\\
&\Leftrightarrow&
\left\{
\begin{array}{l}
0^2-2a \cdot 0-2a+3 \gt 0 \\
2^2-2a \cdot 2-2a+3 \gt 0
\end{array}
\right.\notag
\nonumber\\
\nonumber\\
&\Leftrightarrow&
\left\{
\begin{array}{l}
-2a+3 \gt 0 \\
-6a + 7 \gt 0
\end{array}
\right.\notag
\nonumber\\
\nonumber\\
&\Leftrightarrow&
\left\{
\begin{array}{l}
a \lt \dfrac{3}{2} \\
a \lt \dfrac{7}{6} \\
\end{array}
\right.\notag
\end{eqnarray}
\(\therefore \ a \lt \dfrac{7}{6}\)
これもしっかりメモしておきましょう。
答えを合わせる
さて、やっと3つの条件を揃えることができました。
これらの \(a\) の範囲を全て満たすとき、答えが求められます。

計算量が多い…
目、目が回る…!
\begin{eqnarray}
\left\{
\begin{array}{l}
a \lt -3, 1 \lt a \\
0 \lt a \lt 2 \\
a \lt \dfrac{7}{6}
\end{array}
\right.\notag
\end{eqnarray}

もちろんスピードも大事やけど、高校数学では、与えられる時間も多い。ミスなく計算するのが大事やね。
数直線をかいてみましょう!
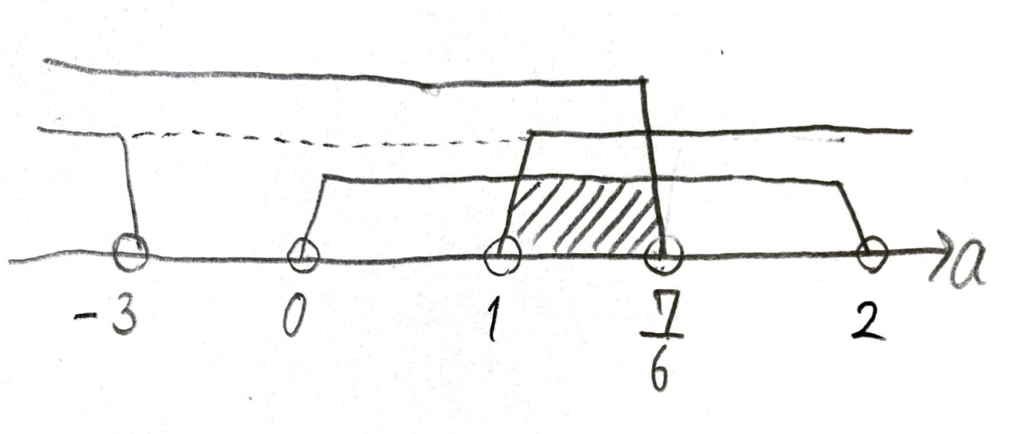
数直線でミスをなくすコツは、あえて均等にメモリを振らないこと。
\(1\) と \(\dfrac{7}{6}\) なんかはあまりに近すぎて、数直線がギュウギュウになってしまいます。
近い数どうしも、広めにスペースをとってあげると良いです。
さて、3つの条件を満たすのは、数直線より \(1 \lt a \lt \dfrac{7}{6}\) です。
これが答え。
ホントに大変でしたね…
ここからわかるように、2次方程式がとある範囲で解を持つとき、3つの条件を満たすのです。
2次方程式がとある範囲で解を持つ
\(\iff\) 3つの条件を満たす
ちょっと踏み込んだことを言えば、2つは必要十分条件の関係にあります。
これは、覚えるべきことです。
それでは、解の配置条件をおさらいしましょう。
- 判別式
→いくつ解を持つのかを調べる - 軸
→解を持つ範囲内に軸が存在することを確かめる(条件として使えないこともある) - 端点
→\(f(x)\) に端点を代入してプラスマイナスを確かめることが多い
なぜ解の配置条件を勉強するのか?
解の配置条件は、難しい問題になればなるほど、まったく関係のない問題と融合して出題されます。
要するに、\(x\) が解を持つか、ということを調べる問題なので、そもそも解を持つかどうかが怪しいことなどよくあることなのです。
小学校の算数や、中学校の数学とは異なり、高校数学ではそもそも答えが存在しないことだってありますし、範囲が極めて限定的なことだってあります。
『少なくとも1つ解を持つ条件』などは、特に計算が複雑なので、難関大学の過去問ではよく見かけます。
以上、現役高校生からの上から目線なアドバイスでした。
まとめ
いやー、本当に大変でしたね。
あとがきですが、わたくしDaddyはこの例題を作成するのに2時間くらいかかってしまいました…
なぜなら、3つの条件を重ね合わせられるようにするのがめちゃくちゃ大変だったからです。
1つでも条件が重ならないと、すぐに『解なし』になってしまうんですよね…
皆さんも、作問者の意図をくみとりながら問題を解くと、面白いかもしれませんね。
学校の先生方や塾の先生方には頭が上がりません…
これからも、受験勉強と両立しながらわかりやすい記事を書いていくので、応援よろしくお願いします!




コメント