
こんにちは。Daddyです。
今回は、一次近似というものを扱っていきます。

ザ・理系って感じの四字熟語だね。
一次近似は、不等式評価の問題でよく問われるテクニックです。
内容自体は全く難しくはないのですが、なんせ思いつくのが難しいです。
ズバリ、使う場面を知ってるか知らないか。
今回も例題を通して、経験値をアップさせましょう!
それでは、Let’s go!
例題を見てみる
ひとまず、一次近似とは何か、を勉強する前に例題を見てみましょう。
こんな問題で一次近似とやらを使います。
次の不等式が正しいことを証明せよ。$$e^{\pi} \gt 21.5$$ただし、\(\pi = 3.14 \cdots, e = 2.71\cdots\) とする。
\(e^{\pi}\) はゲルフォントの定数と呼ばれ、とても有名な数です。
東京大学でも、\(e^{\pi} \gt 21\) を証明して解く定積分の問題が出題されました。
ところで、\(2.71^{3.14}\) は計算できませんよね。
3.14乗は、どう頑張っても計算できなさそうなので、不等式評価が必須です。
試しに \(2.71^3\) を計算してみても、答えは \(19.9025 \cdots\) となってしまいます。
\(21.5\) という数が、大きすぎる壁になっています。
いったい、どうすれば良いのでしょうか?
一次近似の解法
それでは、一次近似をお教えしましょう。
ここで、\(f(x)=e^x\) という関数を考えてみます。
指数関数なので、下に凸のグラフで、単調増加となっています。
\(f( \pi )\) が \(21.5\) よりも大きくなっていれば良いのですね。
とはいえ、我々ができるようなナントカ乗の計算は、整数のみです。
\(f(x)\) には、整数しか代入できません。
仕方ないので、\(x=3\) で考えることにします。
代入する、という意味ではありません。後で説明します。

だからさっきも言ったじゃん!\(2.71^3\) は \(21.5\) よりも小さいの!

焦らんでええやん。まだ一次近似の準備段階や。
お待たせしました、今度こそ一次近似をします!
突然ですがここで、\(x=3\) における接線を引きましょう。
なぜかっていうのは、グラフを見ればわかるでしょう。
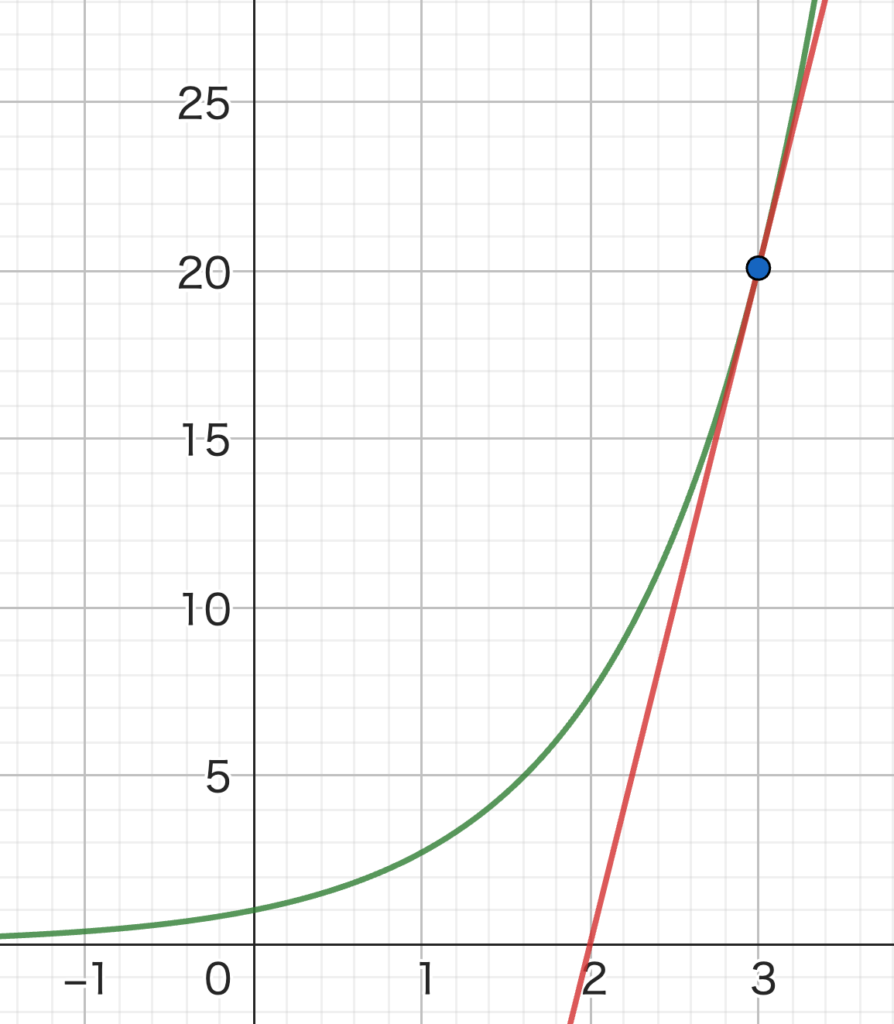
赤い線が \(y=f(x)\) の接線で、青い点がその接点です。
\(x=3\) では、\(y=f(x)\) も接線のy座標も、全く同じ値を示します。

当たり前じゃん。\(x=3\) で接してるんだから。
ここでめっちゃ重要なのは、\(x=3\) の近くでは、\(y=f(x)\) と接線のy座標は、ほとんどおんなじ値であるということです。
上のグラフを見てみたら、\(x=3\) の近くで、緑のグラフと赤のグラフがほぼ重なって見えますよね。
一次近似という言葉はおそらくそれが理由。
もとのグラフで考えにくかったら、求めたい値の近くで接線を引いてみよう!
もとのグラフも接線も、接点の近くだったら大体おんなじ値になるでしょ!
てかもとのグラフも接線も近くで見たら一緒じゃね?!
これが一次近似の考え方です。
\(3\) と \(3.14\) って近くにあるので、接線の方程式に \(x=3.14\) とか代入しても、\(e^{\pi}\) とそんなに変わらない値が出てくるはず。
とはいえ、論理的に不等式で評価していく必要はあります。
まだわからなくても、計算式を眺めればわかることでしょう。
ゴリゴリ計算
それでは、計算フェーズに入ります。
まずは \(x=3\) における接線を求めます。
\(f'(x) = e^x\) で、これが傾きを示します。
\(e^x\) の微分は \(e^x\) で変わらない、ということを思い出しましょうね。
また、接線は \((3, e^3)\) で接するので、この点は通らなくてはなりません。
これだけ丁寧に書けば大丈夫でしょう。
\begin{eqnarray}
y&=&f'(3)(x-3)+e^3\nonumber\\
&=&e^3 (x -2)\nonumber\\
\end{eqnarray}
これが、接線の方程式になります。
ところで、接線は必ず \(y=e^x\) のグラフより下にきます(接点を除く)
グラフを見れば当たり前ではありますが、この根拠は一言添えておくべきでしょう。
ズバリ、『\(y=e^x\) が下に凸だから』です。
これだけ押さえておけば、減点されることはまずないでしょう。
というわけで、いよいよフィナーレ。
不等式を使ってガンガン証明していきます。
\begin{eqnarray}
e^{\pi} &\gt& e^3 (\pi \ – \ 2)\nonumber\\
&\gt& 2.71^3 (3.14-2)\nonumber\\
&\gt& 2.7^3 (3.1-2)\nonumber\\
&=& 21.6513 \nonumber\\
&\gt& 21.5 \nonumber\\
\end{eqnarray}
これで証明完了です!
お疲れ様でした!
ちなみに3行目で、小数の計算を3ケタから2ケタに減らしているのは、計算のテクニック。
まさか3ケタの数を4回もかけ算させるわけないだろう…という希望的観測のもとガバガバに計算したわけです。
もちろん、\(2.71^3 (3.14-2)\) をそのまま計算しても全然OKです。
出てくる値は \(22.688862 \cdots\) となるので、\(21.5\) をオーバーキルしてます。
まとめ
いかがだったでしょうか?
一次近似とは、とある複雑な関数があって直接値を求めるのが難しい時に、その付近で接線を引いて一次関数として大まかな値を知る、というテクニックです。
一次近似を使うためには、その関数が微分可能である必要がありますが、曲線の関数や、無理数の不等式評価の問題などでは大変有用です。
曲線関数も接線も、近づいてみたら大体おんなじ値出るっしょ!というテンションで使ってみましょう。
それではっ!

ちなみに、\(e^{\pi}=23.14069\cdots\) やで。



コメント