こんにちは。
毎度おなじみDaddyです。
今回は、三角比についてのお話ですね。
私は中学生の頃、数検の勉強で三角比が出てきて、めっちゃ萎えた記憶があります。

あんなの、中学生がやるもんじゃねえええええええ!
でも大丈夫。
この記事をしっかりと読めば、なぜsin,cos,tanが90°以上でも使えるのか、必ず理解できるようになります。
ぜひ丁寧に読んでいってくださいね。
それでは、Let’s go!
復習:三角比とは

三角比ってなんだっけ?

高校で学習する、角度を表す方法のことやな。
軽く復習してみましょう。詳しくは触れません。
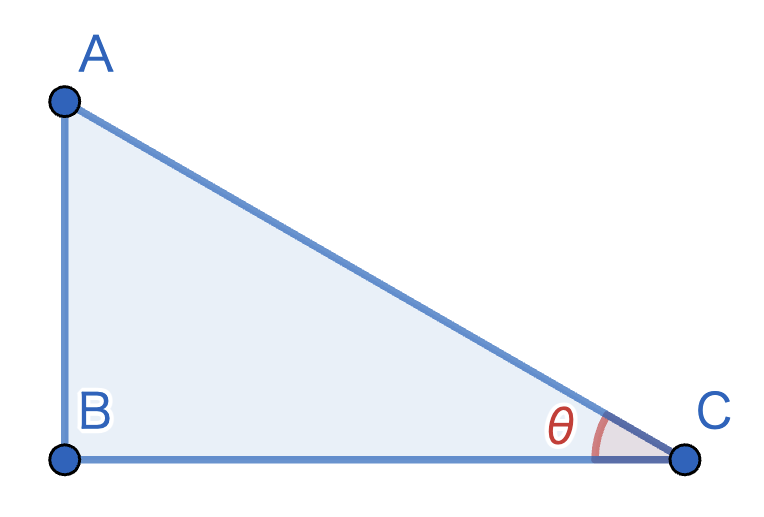
三角比は、次のように表すことができます。ただし、\(\angle B\) は \(90^{\circ}\) です。また、\(\theta\) は角度を表すギリシャ文字です。
\(\sin \theta = AB \div AC\)
\(\cos \theta = BC \div AC\)
\(\tan \theta = AB \div BC\)
三角比そのものっていうのは、別にすごいものでもなんでもないです。
ですが、sin,cos,tanのグラフにはとっても面白い性質があり、とっても広い分野で活躍します。
『なんでこんなこと勉強しなきゃならないの〜』と思うかもしれませんが、これは将来への投資だと思ってください。
これからの高校数学は、とっても面白いものです。
三角比を広げよう
それでは、三角比についてちょっと深ぼってみましょう。
三角比って今のままだと超不便!

ちょっと考えてみてください。
『\(\sin 30^{\circ}\) はいくつですか?』と聞かれたら、『\(\dfrac{1}{2}\)です!』と答えられますよね。
\(\cos 71^{\circ}\) とか言われても、手では計算できなくてもコンピューターとかに測ってもらえそうですよね。
じゃあ、\(\tan 120^{\circ}\) はいかがでしょう?
一度手を止めて、考えてみてください。

は?そんなのないよ。

せやねん。sinとかを直角三角形で定義してしまった以上、\(\tan 120^{\circ}\) っていうもんは無いんや。
そこで、諦めたくない数学者は考えました。

これさ、90°以上の角や、マイナスの角でも三角比使いたくね?使おうよ。

いや、それが無理だって言ってるでしょ?

じゃあさ、sinの定義変えたら良いじゃん。良くね?
はい、発想がぶっ飛んでます。
せっかく覚えた三角比の定義、一瞬にして無駄になりました()
それでは次のセクションで、新しい三角比を勉強しましょうか…
※ これまでの三角比の定義は、これからもバンバン使います。上の言い方は大袈裟です。決して無駄にはなりません。ただ、三角比の定義が広くなるのは事実です。
単位円
さて、ぶっ飛んだ数学者は『単位円』とかいうものを作りました。
何かというと、半径が1の円のことです。
中心は原点Oに一致しています。

げ、原点ってお前、まさか…

ん?原点ってあの原点よ。
xとyのグラフを作るときに出てくる『原点』よ。
これからは『図形』ではなく、『グラフ』として見ていきます。
ぶっ飛んでますね。
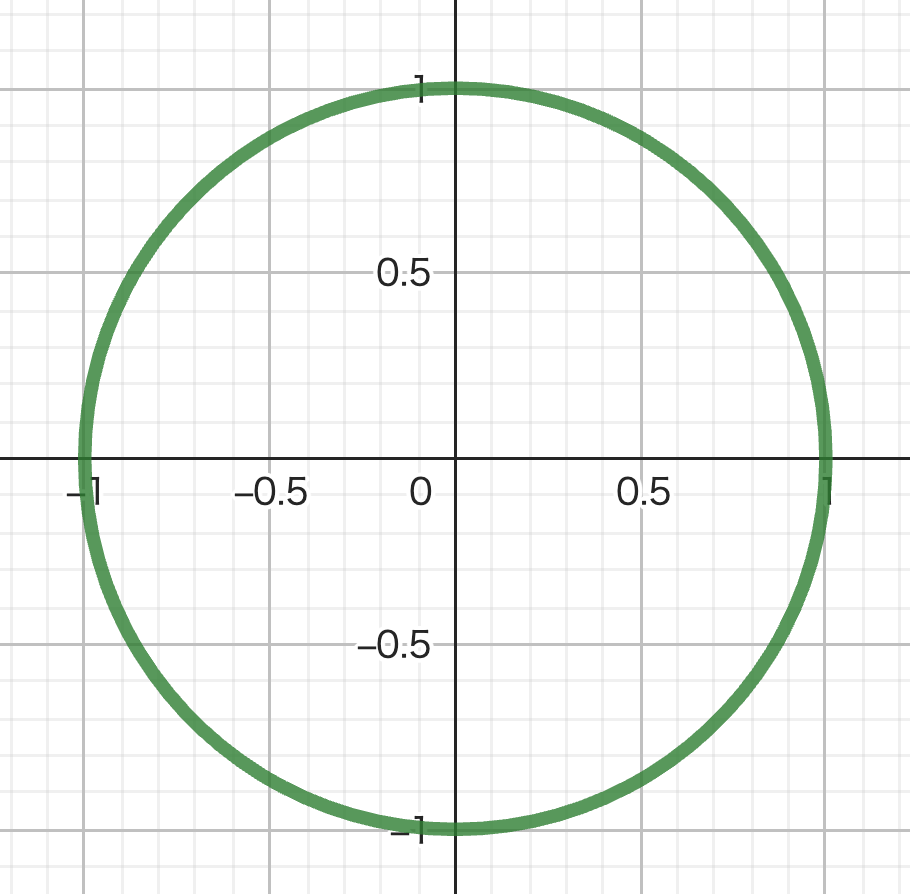
これ、半径が1であるというのがめっちゃ大事なんですよね。
さて、角度 \(\theta\) を次のように決めてみましょう。
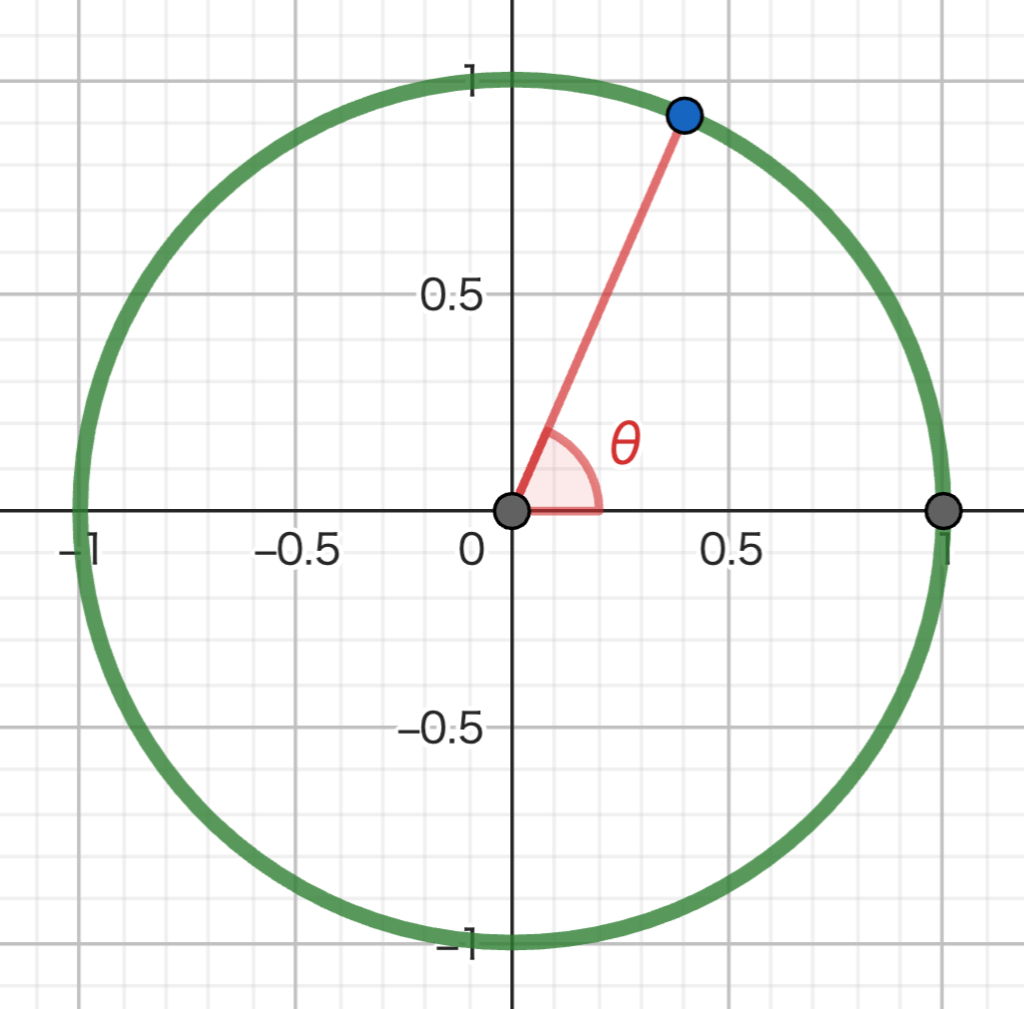
\(\theta\) っていう文字そのものに拒否反応を起こす人がいますが、これはただの角度を表す文字。
嫌な人は別の文字を使っても良いですよ。
(\(x,y\) はあとで使うからやめてね)
さて、下のように直角を作ります。要するに、垂線をおろしてるだけです。
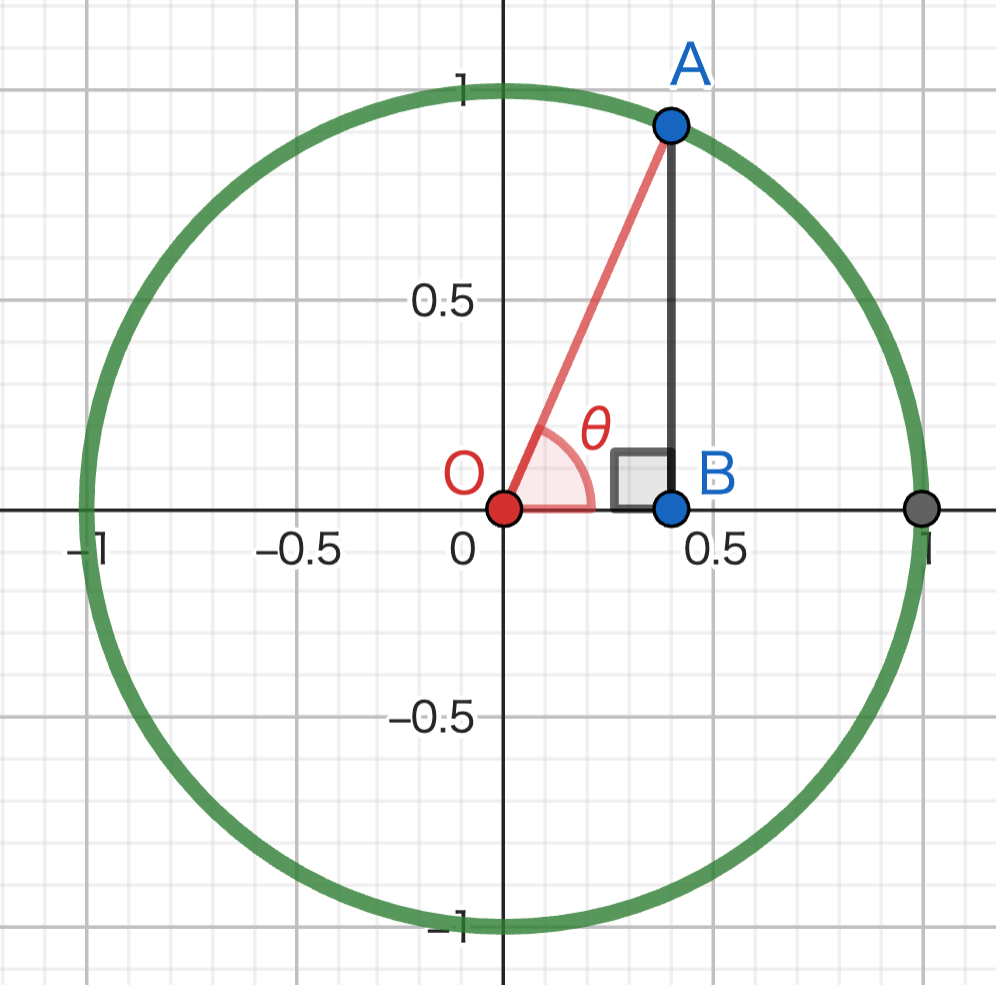
さて、ちょっと難しい問題。
上の直角三角形で、\(\sin \theta\) と \(\cos \theta\) はどこにあるでしょうか?
ちょっと質問の意味がわからないかもしれないですね。
下の式の意味がわかれば十分です。
\(\sin \theta = AB \div OA\)
\(\cos \theta = OB \div OA\)
これは三角比の定義ですので、流し読みせずちょっと立ち止まって読めばすぐに理解できるはずです。
そして、ここからが本題。
\(OA\) の長さっていくつでしょうか?

\(OA\) って、よく見たら単位円の半径になってるね。

めっちゃええことに気づいたやん。てことは長さは1やね。
単位円の定義を覚えていますか?
半径が1の円のことです。(原点中心の条件もありますが、ここでは割愛)
つまり、先ほど求めた \(\sin \theta, \cos \theta\) の式に、\(OA=1\) を代入すると…
\(\sin \theta = AB \div 1 = \color{red}{AB}\)
\(\cos \theta = OB \div 1 = \color{red}{OB}\)
\(\sin \theta = AB, \cos \theta = OB\) という驚きの事実が得られました。

ついてきてるか?ここで、点Aの座標について考えよう。
まずは、Aのx座標を考えます。
x座標の長さは、直角三角形で考えると、OBに当たります。
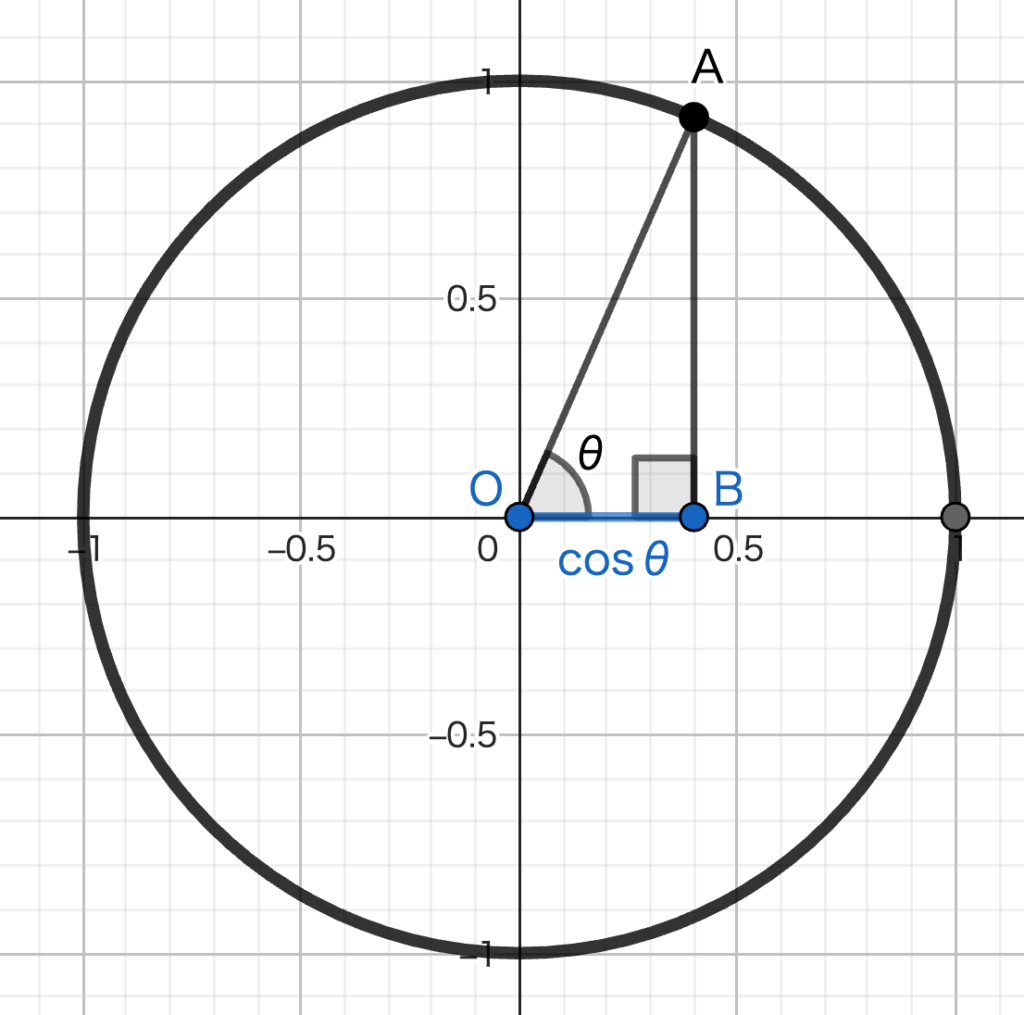
\(\cos \theta = OB\) と求めたことを覚えていれば、Aのx座標は \(\cos \theta\) となりますね。
同様にして、y座標も求めます。
\(\sin \theta = AB\) ですから、Aのy座標は \(\sin \theta\) となるのです。
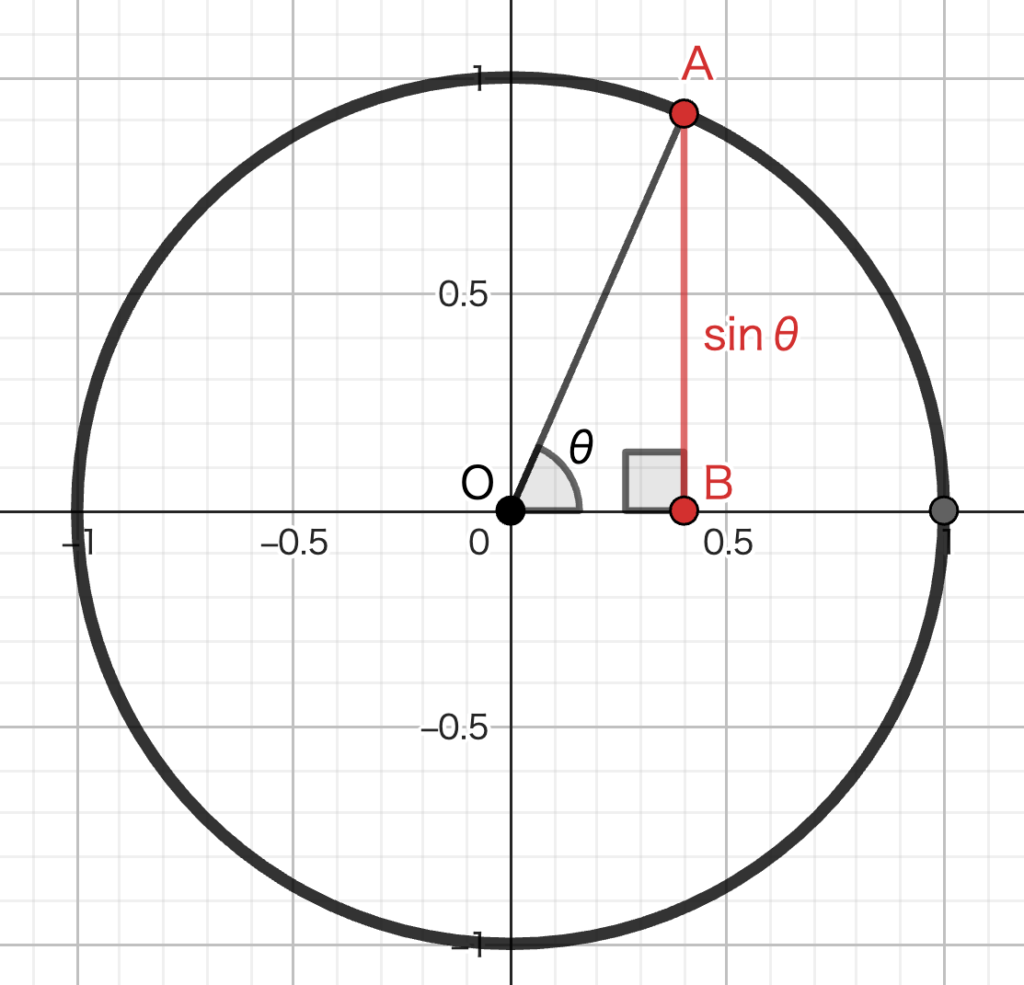

んーと、Aの座標が求まったね。なんだっけ。

\(A(\cos \theta, \sin \theta)\) になるんやな。びっくりや!
\(\cos \theta, \sin \theta\) は、単位円の上にある点のx座標とy座標に対応しています。
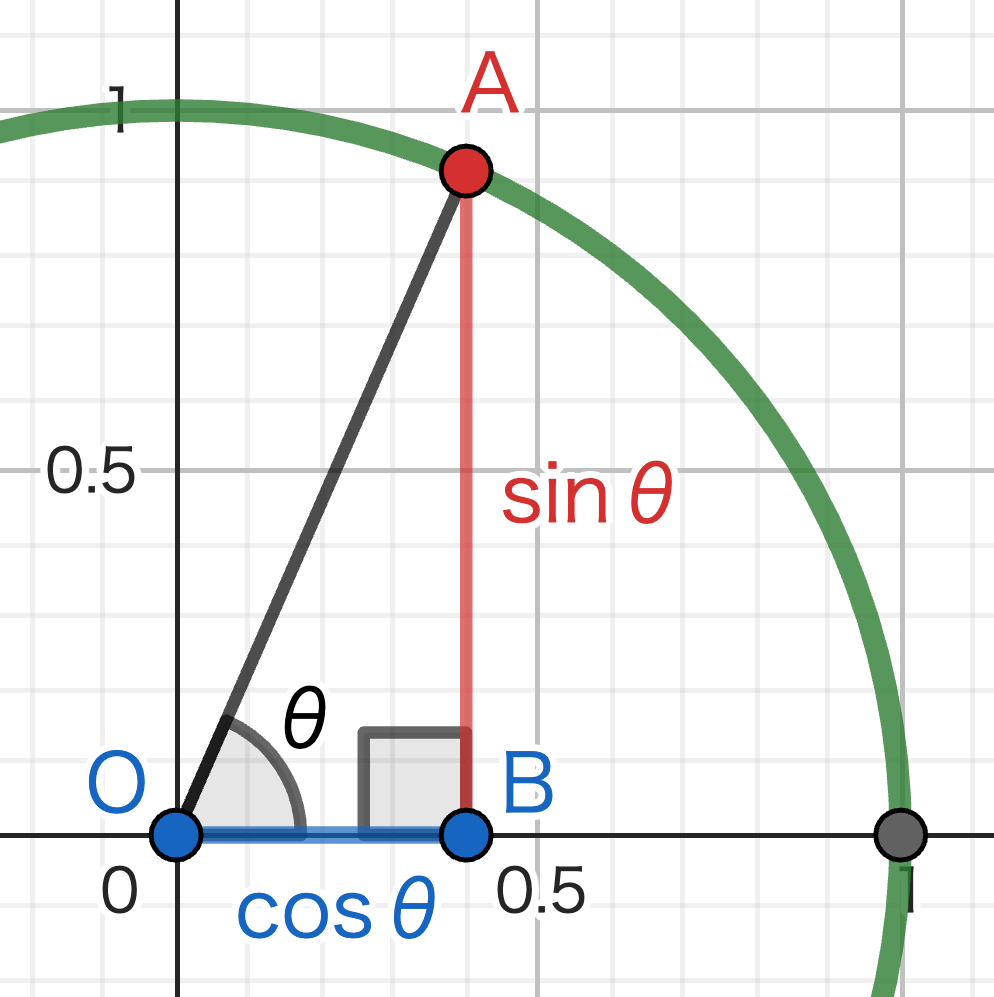

とりあえず、準備段階はこれでクリア。\(\tan \theta\) とかはちょっと待っててな。
いよいよ本題!90°以上の三角比

いやー、ついにこの時が来たか!
さっきの定義から見直して見ましょうか。
もうあなたは直角三角形でsin,cosを考える必要がありません。
単位円で考えれば良くなりましたね。
つまり、角度に制限はなくなったのです!
下のGIF動画を見てください。
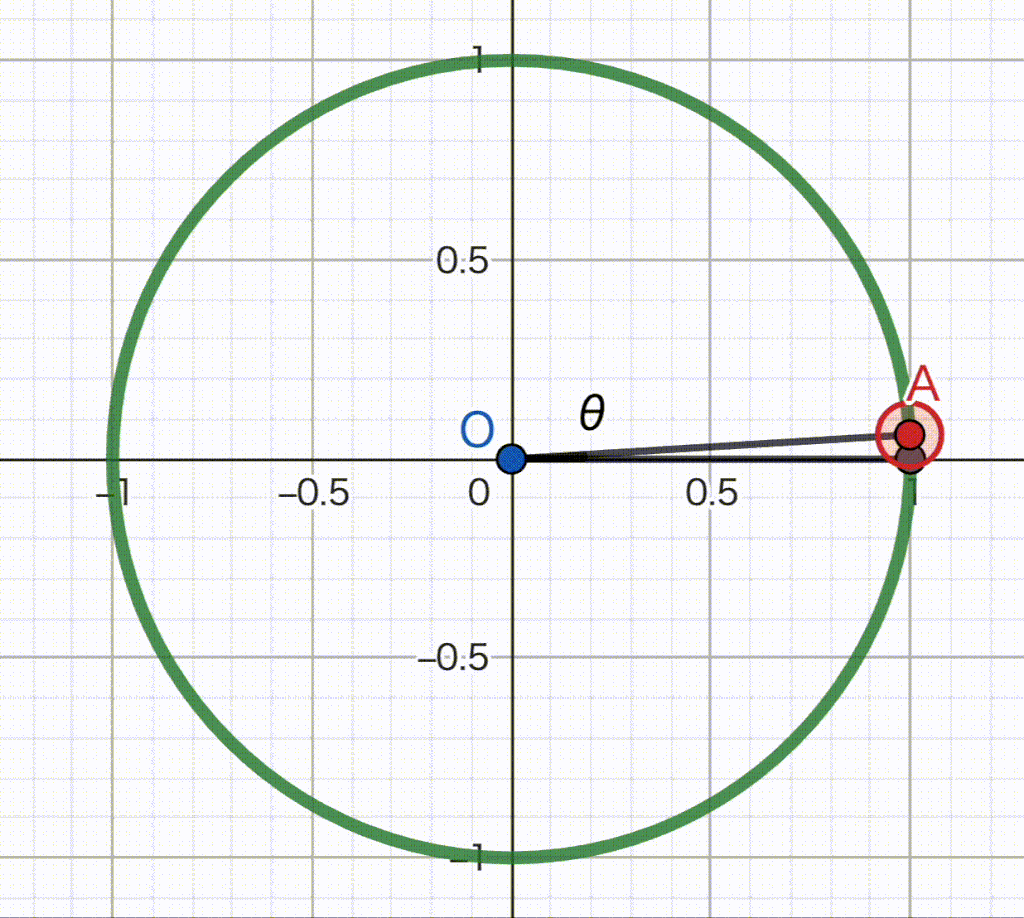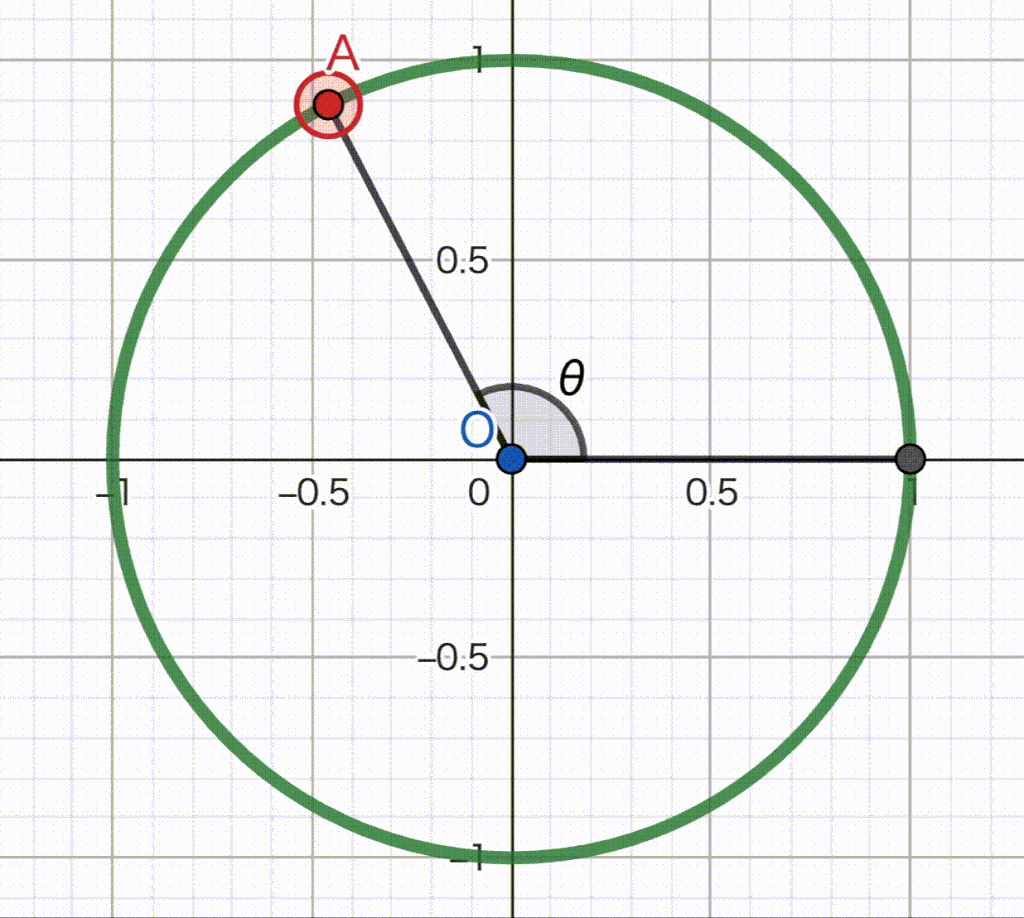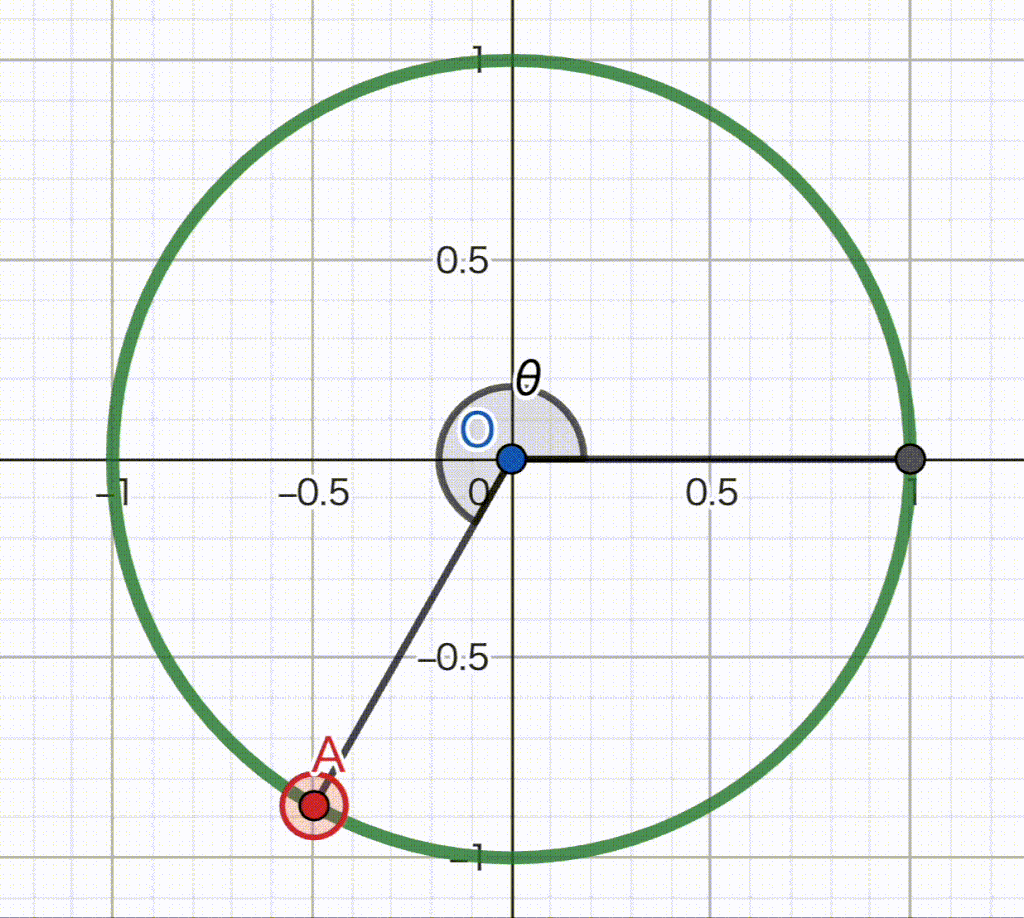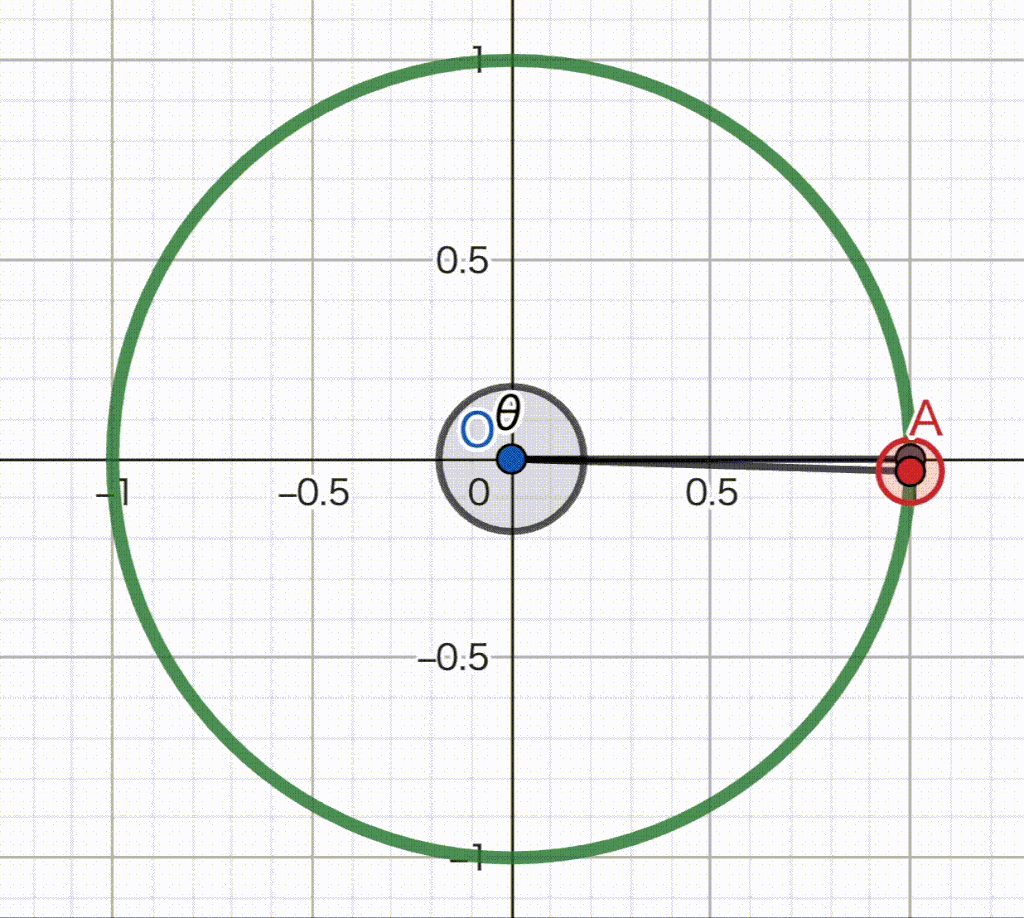

パソコン初心者高校生が作るにはちょっと難しかった…
さて、この動画では、\(\theta\) が刻々と大きさを変えています。
中には、\(\theta\) が90°以上の時もあります。
それぞれの \(\theta\) において、直角三角形を考える必要はありません。
それぞれの点でのx座標とy座標だけを見てください。
x座標がcosを、y座標がsinを表しています。
sinやcosは-1から+1までの範囲を行ったり来たりしていることがわかりますね。
正確な求め方はまだ教えていませんが、たとえば \(\theta = 210^{\circ}\) のとき、\(\sin 210^{\circ} = -\dfrac{1}{2}\) くらいだな〜ということが動画からわかると思います。
繰り返しますが、\(\sin \theta, \cos \theta\) の値を求めるときには、単位円のx座標とy座標だけを見てください。
補足:三角比の相互関係の公式
みなさんの中で、三角比の予習が済んでいる人がいるかもしれません。
次の3つの公式を完璧に覚えていますか?
- \(\sin ^2 \theta + \cos ^2 \theta = 1\)
- \(\tan \theta = \dfrac{\sin \theta}{\cos \theta}\)
- \(\tan ^2 \theta + 1 = \dfrac{1}{\cos ^2 \theta}\)
実はコレ、万が一忘れてしまってもすぐに思い出すことができる方法があるんです。
これは、単位円の考え方をマスターしていればすぐに理解できます。

まーた単位円じゃん。良い加減にしてよ。

せやけど、上の公式全部覚えたいか?あと、\(\tan \theta\) の解説終わってへんがな。
\(\mathsf{sin^2 \theta + cos^2 \theta = 1}\) の公式
まずはこの式。
三平方の定理で全てが解決します。

おなじみの画像ですね。
三平方の定理を使って、この式を作ってみましょう。

三平方の定理って、\(a^2+b^2=c^2\) だよね。
その通り。
ここで、斜辺の長さを考えましょう。
OAのことです。
OAは言うまでもなく、半径のことですから、長さは1。
他の2辺の長さは、\(\cos \theta, \sin \theta\) です。
これらは直角三角形の辺々です。
よって、三平方の定理から、\(\sin^2 \theta + \cos^2 \theta = 1\) が求まりました!
\(\mathsf{tan \theta = \dfrac{sin \theta}{cos \theta}}\) の公式
次はこの式。
これは、tanの定義と単位円から求められます。
tanは、直角をつくる2辺の長さから求められますよね。

あとはtanを求めるために、割り算をするだけ。
\(\tan \theta = \dfrac{\sin \theta}{\cos \theta}\) で完了!
\(\mathsf{tan^2 \theta + 1 = \dfrac{1}{cos^2 \theta}}\) の公式
最後に、この式。
これだけは、単位円では求められません…

え?じゃあ無理じゃん笑
いやいや、少しだけ待ってください。
この公式を導き出すのに必要なのは、次の式です。
\(\sin^2 \theta + \cos^2 \theta = 1\)
これはさっき求めましたよね?
1つ目の公式です。
これ、両辺を \(\cos ^2 \theta\) で割ってみてください。
\begin{eqnarray}
\sin^2 \theta + \cos ^2 \theta &=& 1 かつ \cos \theta \neq 0\nonumber\\
\nonumber\\
\iff \dfrac{\sin^2 \theta}{\cos ^2 \theta} + 1 &=& \dfrac{1}{\cos ^2 \theta}\nonumber\\
\end{eqnarray}
もう1つだけ使わせてください。
2つ目の公式です。
\(\tan \theta = \dfrac{\sin \theta}{\cos \theta}\)
これを、さっきの式の一番左に代入して、整理してみましょう。
すると、
\(\tan^2 \theta + 1 = \dfrac{1}{\cos^2 \theta}\)
確かにその場で求められることがわかりましたね。
3つ目の公式を求めるには、1,2つ目の公式を知っていれば良いと言うわけ。
結局、単位円が全てを解決します。
まとめ
いかがだったでしょうか?
今回は、sin,cos,tanが90°以上でも使える理由について解説しました。
一度単位円を作れば、sin,cosの値を座標で考えることができます。
この考え方であれば、θが90°以上でも良いし、角度の取り方を時計回りにすれば、マイナスの角度でも算出することができます。
また、単位円を作ることで、相互関係の3つの公式を瞬時に作ることができる、と言うのも大きなメリット。
単位円という言葉だけでも覚えて帰ってください。
それではっ!



コメント