こんにちは!shuです。
今回は数学の入り口でもある、マイナスについて一緒に学んでいきましょう。
まずマイナスの話をする前に、数学の世界での数の分類について学びます。
下の図が、これから学ぶ数の全体像になります。
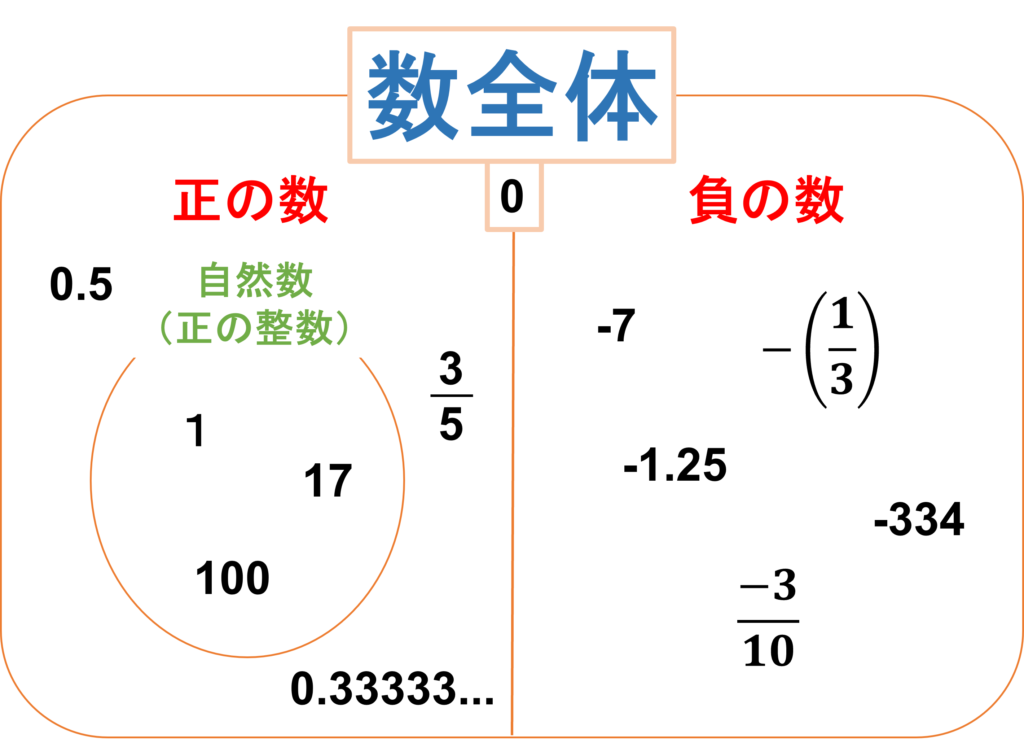
今回新しく覚えてほしい言葉は3つです
自然数
自然数とは、1,2,3,..のように、0よりも大きな整数のことを言います。したがって、0は自然数
ではなく整数のくくりになります。
おすすめなのは、1個、2個…のようにものを数えるときに使う数を自然数と覚えることです。
(りんごが0個ある、とは言いませんから、0は含みません)
正の数(すう)
0よりも大きな数のことを、すべて正の数といいます。\(1,2,10,5.5,\dfrac{3}{5}\)など、0よりも大きければ(0は含まない)正の数です。
実は、今挙げた数字の前にはあるものが隠れています。それが+(プラス)です。本当は正の数には
+1,+2のように数字の前にプラスが付きます。ちなみに、数字の前にくる+(プラス)または
-(マイナス)の記号のことを、符号といいます。正の数には、+(プラス)という符号が隠れて
います。では、これから数を書くときはわざわざ符号をつける必要があるのでしょうか?
ご安心ください
数学の世界では通常、+は省略可能とされています。いちいち書くのが面倒くさいからですね笑
(これから学習する-(マイナス)は必ずつけなければいけませんが…)
ですので、3も+3も同じ数になります。(ちなみにこれから先、めったに+3と書かないです)
ここで注意してほしいのが、数字の前に来る+や – と足し算や引き算で使われる+や – は、
全然別のものです。前者は符号、後者は記号になります。ですから、2+(+3)のように
表記されても混乱しないようにしてください。最初の2は符号の+が省略されていて、
次の+は足し算の記号、つぎの+は3につく符号で、+3で一つの数になっています。
大体計算式などで+を省略しないで書く場合、上の例のように()で表記することが多いです。
負の数(すう)
正の数とは反対に、0よりも小さい数のことを負の数といいます。こちらも正の数同様、
0は含まないので注意してください。(0は正でも負でもないどっちつかずな数ですね笑)
\(\displaystyle -1,-108,-0.333…,-\frac{7}{10} \)など、0より小さい数はすべて負の数です。
負の数は、先ほどからちょくちょく登場している-(マイナス)を数字の前につけて表します。
当然ですが、+の時と違って、-は省略できないので注意してください
ところで0より小さい数と言われて、あまりピンとこない人もいるかもしれません。
でも実は、マイナスって日常生活の中に紛れ込んでいるんです。
例えば気温は、めちゃくちゃ寒いところでは0℃を下回ると-〇℃のように表記されます。
あとは標高も、海面より低い地域では標高-〇mのように表されているなど、日常でも使われて
いるのがマイナスなのです。
整数
今度は小学校でならった整数です。じつは整数は、正の数だけでなく負の数にも適用されるんです。
整数は、0,1,2,3,…に加えて-1,-2,-3,…も整数になります。ここで、整数は自然数と違って
0をふくむことに注意してください。あくまで自然数は数えるときに使う数ですよ!
また、今まで習ったことと組み合わせると、自然数は正の整数、-1,-2,-3,…は負の整数と
表すこともできます。
復習を兼ねて問題を解いてみましょう。
問題演習
次の数について答えなさい
\(3.6, -2, +\dfrac{6}{7}, 0, 7, -1.666…, \dfrac{1}{-5}, 3.14159…\)
↑スクロール可能
(1)自然数であるものを答えなさい
(2)整数であるものをすべて答えなさい
(3)正の数であるものをすべて答えなさい
(4)負の数であるものをすべて答えなさい
(1) \(7\)
自然数は、数えるときに使う数、いわゆる正の整数です。この中だと7しかありません。0は含まないことに注意してくださいね。
(2) \( -2, 0, 7\)
ここでは分数や小数になっていないものを選びましょう。中学校二年生までは、整数は分数または小数でないもの、という認識でOKです。(中三からはまた新しく数の拡張をしますのでおたのしみに!)
(3) \(3.6, +\dfrac{6}{7}, 7, 3.14159…\)
正の数は、0より大きな数で、0を含めないんでしたね。ですから、上の4つの数が答えとなります。ここで、符号である+はつけてもつけなくても同じ数になることに注意してください。
(4) \(-2, -1.666…, \dfrac{1}{-5}\)
負の数は、0より小さい数で、こちらも同様0を含めないんでしたね。ですから、上の3つの数が答えになります。負の数は必ず – がつくのでわかりやすいですね。
ここからは余談なのですが、自然数に0を含めた数(0,1,2,3,4,…)を言いたいときは、
負ではない整数、すなわち非負整数と表すことがあります。中学数学ではほとんど出てこない
言い方ですが、今後、問題を解いて答案を作るときに便利になるのでおぼえておいて
損はないかもしれません。
まとめ
今回学んだ数の分類について、もう一回全体像を押さえておきましょう
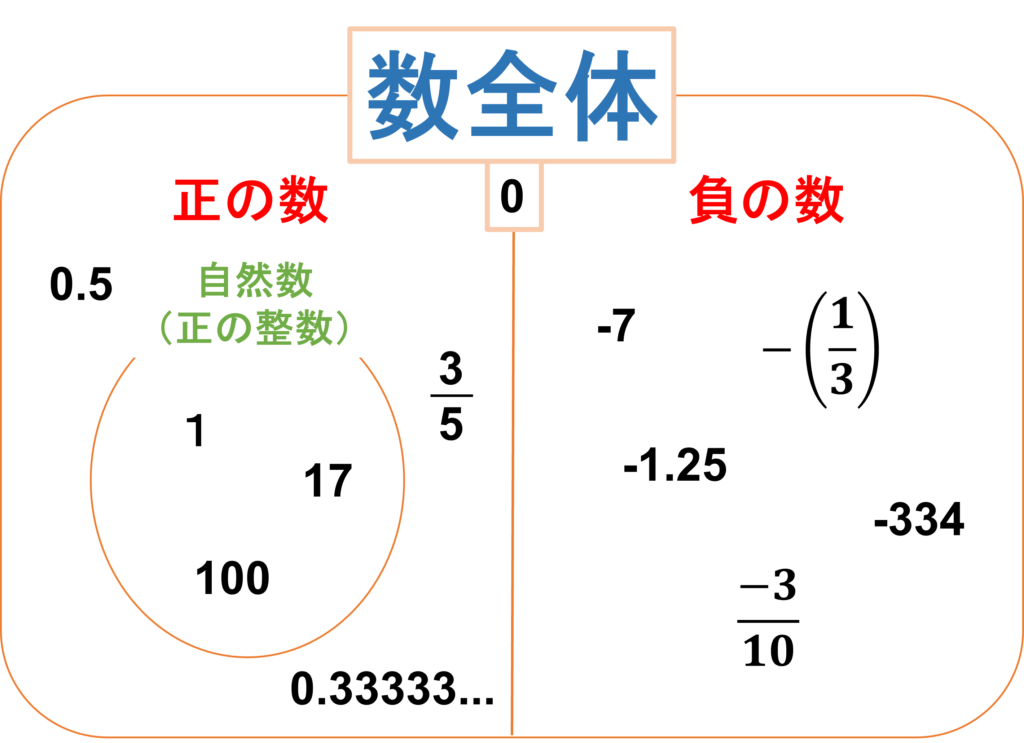
今まで正の数しか使えなかったため、例えば2-5のような計算はできませんでした。
しかしマイナスを導入することで、そのような計算ができるようになり、世界が広がりました。
このように、これから先の数学では新しい概念を導入して世界を広げることがたくさんあります。
そうしてできることが増えていく感覚が、数学の醍醐味の一つです笑
次回は、数の大小について学びます。ではさようなら!




コメント