箱ひげ図ってナニ？読み方からすべて現役高校生が分かりやすく解説！

こんにちは。Daddyです。

みなさんは日常生活で統計をとりたくて仕方がないときはありますか？（あるわけがありません…）

GIGAスクール構想なんてのも始まって、パソコンはおろか統計を正しく扱えるスキルはもはや当然のように身につけなければならなくなりました。

箱ひげ図を中学校で丁寧に学習するようになったのも実は最近のことです。

ネットを調べても中学生向けのわかりやすいサイトはあまりないので、ここでしっかりまとめておきます。

それでは、いきましょう！

四分位範囲とは？

四分位範囲とは、データの散らばりぐあいを示すための範囲です。

計算式は、\((第3四分位数)-(第1四分位数)\) です。

『なんのことかわからん』という人は、下の記事で勉強してみましょう。（3分くらいで読み終わります）

外れ値についても扱っています。

箱ひげ図のつくり方

さて、ここからがメイン。

箱ひげ図は、冒頭の画像のように、1つの箱から2本のひげのようなものが出ている図のことです。

使用する値は、次の5つ。

これに加えて、たまに外れ値を扱う問題もあります。

それでは作成手順を紹介します。

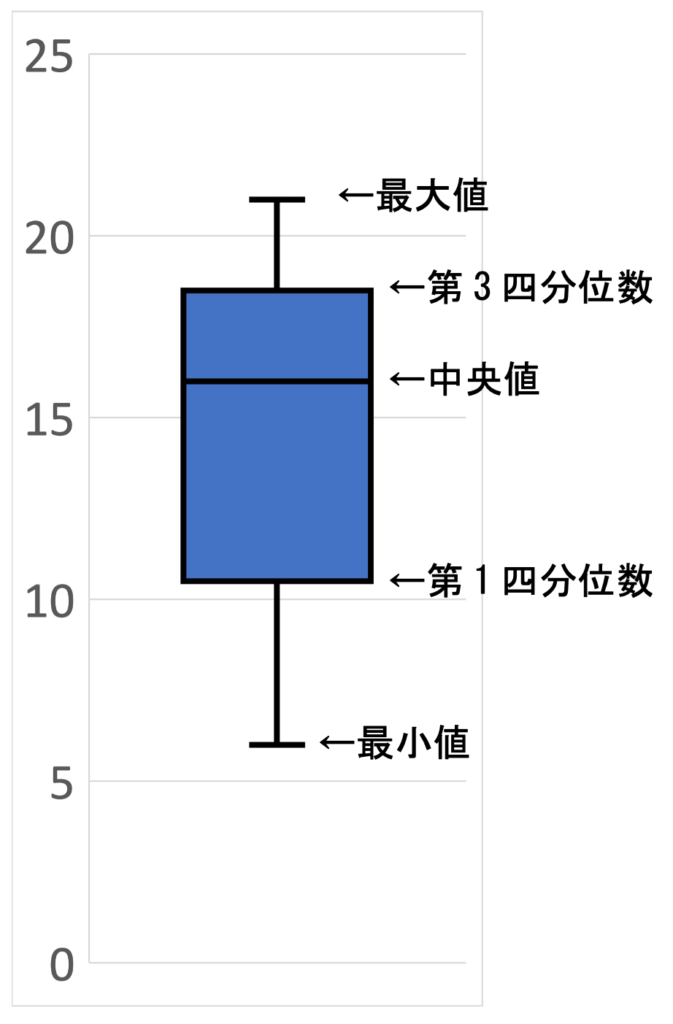
まずは使用する5つの値を求めましょう。

最大値は6、最小値は21となりますね。

次に、四分位数を求めます。

第2四分位数（中央値）を求めたいですが、ちょうど真ん中のデータはないので、真ん中2つのデータ15, 17の平均で代替します。よって16です。

第1四分位数は、前半のデータ6, 9, 11, 12, 15の中央値なので、11です。

第3四分位数は、後半のデータ17, 17, 18, 20, 21の中央値なので、18です。

これで準備は整いました。

次のように、箱とひげを書いて完成です。（色は塗っても塗らなくても良いです。）

外れ値が含まれる場合は、まず初めに外れ値を除外したデータだけで四分位数などを求め、箱ひげ図を作ります。

その後、外れ値のところにバツ印または＊を打ちます。

箱ひげ図でわかること

箱ひげ図は、データの散らばりを視覚的に捉えるために作ります。

先ほど作ったグラフでは、データが大きい数の方にやや偏っていることがわかります。

グラフがぎゅっと縮まっているほど、そこに偏っていると言えます。

また、四分位範囲を箱で表しているので、中心となるデータが明確になります。

最大値や最小値も、データそのものの範囲を指定する上で重要ですが、データの傾向を掴んだり、いわば『普通とは何か』を定めるためには四分位範囲が便利です。

発展：外れ値はどうやって決める？

ところで、外れ値はどうやって決めるのでしょうか？

数学は厳密さを追求する学問ですので、『なんとなく外れ値っぽい』というだけでは、どのくらい外れた値なのかがわからず、データとしての価値を失います。

高校数学以降では、有意水準などの考え方を用いることで、『この条件を満たせば外れ値である』という誰もが納得のいく基準を何種類か設けることができます。

とはいえ、これらは中学数学の範囲ではないので、興味があったらさらに調べるくらいのスタンスで構いません。

標準偏差を使う方法

まずは標準偏差を使う方法。

この値は \(\sigma\)（シグマ）という文字を使って表されることが多いです。

カンタンにいうと、標準偏差 \(\sigma\) はデータが平均値と比べてどれだけバラついているかを数値にしたものです。

皆さんは、偏差値を求めるときに知らぬ間にお世話になっています。

多くの場合、平均との差が \(3\sigma\) 以上のデータを外れ値とみなします。

偏差値で言い換えると、偏差値が20以下または80以上のデータを外れ値とみなすわけです。

確かに、偏差値80以上は上位0.13%の人しか取ることができないので、滅多に見ることはありませんよね。

確率的には『外れ値』とみなして良いわけです。

四分位範囲を使う方法

もう一つは、四分位範囲を使う方法。中学校ではこれが主流だと思います。

とある統計学者が、外れ値を次のように定義すると便利であることを提唱しました。

ここでのポイントは、『この値、外れてるなー』という感覚を四分位範囲×1.5という値で明確に定義したということ。

標準偏差を求める計算は、実は非常に難解でありながら計算量も膨大です。

そのため、簡易的にこの方法を用いることが多いです。

まとめ

いかがだったでしょうか？

箱ひげ図は、もしかしたら中学校教育ではおろそかにされてしまうかもしれませんが、今後レポートを書くような機会があれば、データを視覚的にまとめるための必須スキルです。

何度も作って、知識を定着させてください。

それではっ！