
こんにちは。Daddyです。
今回は、統計に関するキホンの内容を勉強していきます。
数学というよりも、覚えること中心の単元になりますが、将来テクノロジを活用して仕事をするためには、欠かせないものとなりますので、ぜひ最後まで読んでください。
それでは、いきましょう!
スマホでこの記事を閲覧している場合、数式や表が枠内に入りきっていないことがあります。スクロールをお試しください。
中央値って?
まずはキホン中のキホンである中央値を覚えましょう。
中央値とは、データを小さい順に並べたとき、真ん中にくるデータのこと。
数学で扱うデータは、身長、体重、体力測定の記録など、数字で表せるもののことを普通指します。
ここで、平均値との違いを見てみましょう。
平均値には、平均値を求めるための数式が存在します。
データを全て足して、個数で割るというものですね。
ところが、中央値を求める計算式は存在せず、
また、1つのとんでもなく値の大きなデータや欠損したデータが含まれる場合でも、中央値はその悪影響を受けづらいという性質があります。
次の例を見てみましょう。
次のデータの平均値と中央値を求めよ。
| 21 | 23 | 24 | 25 | 27 | 28 | 23876 |
ほとんどのデータは25くらいの値ですが、最後だけ跳ね上がってます。
平均値と中央値の最大の違いは、このように傾向から外れた値である外れ値に影響されるかどうかというところにあります。
平均値を求める。
\(\dfrac{21+23+24+25+27+28+23879}{7}=\color{red}{2432}\)
次に、中央値を求める。真ん中の数を求めれば良いので、\(25\)
平均値は、極端な外れ値の影響を大きく受けてしまいます。
実際に、先ほどの例題では平均点がとんでもなく大きな数になってしまっています。
一方で中央値は、極端な外れ値があっても、全体的な傾向をそのまま反映させることができます。
覚えなければならない性質ではありませんが、『なぜ平均値ではなく中央値を使うのだろう』という場面が来たときは、これで納得してください。
四分位数とは?
ただ、中央値だけを扱っていても、正確なデータの分析はできません。
もう少しデータの範囲を細かく区切って、その中で何種類か中央値を求めたい場面が存在します。
数学では、3つの数を使ってデータを4分割していきます。
この『3つの数』のことを四分位数と言います。
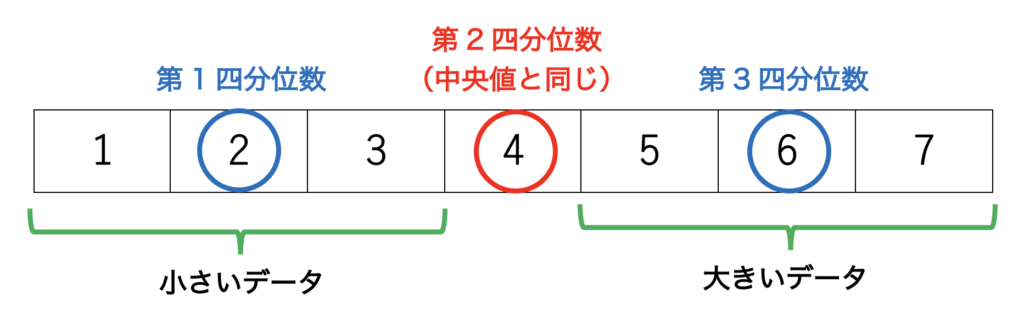
3つ数が存在するので、第1四分位数、第2四分位数、第3四分位数という言い方をします。
とはいえ、これらの数の定義を、問題演習なしに理解するのは至難の業。
データが偶数個のときの中央値の扱いなどは複雑です。
例題を通して、具体的に学んでいきましょう!
次のデータについて、最小値、四分位数、最大値を求めよ。
(1) 7人の生徒が跳び箱のテストで跳んだ段数
| 生徒名 | A | B | C | D | E | F | G |
| 段数(段) | 5 | 6 | 6 | 7 | 7 | 8 | 9 |
(2) 8人の生徒における50m走の記録
| 生徒名 | い | ろ | は | に | ほ | へ | と | ち |
| 秒数(秒) | 6.4 | 6.9 | 7.2 | 7.4 | 7.6 | 8.0 | 8.1 | 8.9 |
(3) 道端で見かけた11人の身長の記録
| アンケートID | F1 | P5 | Q2 | B4 | R9 | A0 | E3 | W7 | N6 | S8 | C2 |
| 身長(cm) | 176 | 167 | 154 | 172 | 180 | 179 | 173 | 178 | 150 | 145 | 165 |
ここで新たな統計量である最小値、最大値が出てきたので紹介します。
最小値、最大値はデータを小さい順に並び替えたときにそれぞれ最も小さいデータと最も大きいデータの値のことを指します。
名前の通りなので、あまり深掘りする必要もありませんね。
(1) データはすでに小さい順に並んでいる。
| 生徒名 | A | B | C | D | E | F | G |
| 段数(段) | 5 | 6 | 6 | 7 | 7 | 8 | 9 |
最小値は \(5段\) で、最大値は \(9段\) となる。
中央値(第2四分位数)は \(7段\) となる。
次に、中央値より左側のデータだけで考える。
| 生徒名 | A | B | C |
| 段数(段) | 5 | 6 | 6 |
このデータの中央値が第1四分位数になるので、\(6段\)
同様に、中央値より右側のデータだけで考える。
| 生徒名 | E | F | G |
| 段数(段) | 7 | 8 | 9 |
このデータの中央値が第3四分位数になるので、\(8段\)
(2) データはすでに小さい順に並んでいる。
| 生徒名 | い | ろ | は | に | ほ | へ | と | ち |
| 秒数(秒) | 6.4 | 6.9 | 7.2 | 7.4 | 7.6 | 8.0 | 8.1 | 8.9 |
最小値は \(6.4秒\) で、最大値は \(8.9秒\) となる。
次に、中央値(第2四分位数)を求める。
ちょうど真ん中の数は存在しないので、真ん中にある2つの数の平均を取ることにする。(今回なら \(7.4\) と \(7.6\) の平均)
よって、\(7.5秒\)
ここで、中央値より左側のデータだけで考える。先ほど中央値を求める時に使った \(7.4\) は、中央値ではないので、このデータに含めて良い。
| 生徒名 | い | ろ | は | に |
| 秒数(秒) | 6.4 | 6.9 | 7.2 | 7.4 |
このデータの中央値が第1四分位数になるので、先ほどと同様に、真ん中の2つの数の平均をとって、\(6.65秒\)
同様に、中央値より右側のデータだけで考える。先ほど中央値を求める時に使った \(7.6\) は、中央値ではないので、このデータに含めて良い。
| 生徒名 | ほ | へ | と | ち |
| 秒数(秒) | 7.6 | 8.0 | 8.1 | 8.9 |
このデータの中央値が第3四分位数になるので、先ほどと同様に、真ん中の2つの数の平均をとって、\(8.05秒\)
(3) データを小さい順に並び替えると、次のようになる。
| アンケートID | S8 | N6 | Q2 | C2 | P5 | B4 | E3 | F1 | W7 | A0 | R9 |
| 身長(cm) | 145 | 150 | 154 | 165 | 167 | 172 | 173 | 176 | 178 | 179 | 180 |
最大値は \(145cm\) で、最小値は \(180cm\) となる。
中央値は \(172cm\) となる。
次に、中央値より左側のデータだけで考える。
| アンケートID | S8 | N6 | Q2 | C2 | P5 |
| 身長(cm) | 145 | 150 | 154 | 165 | 167 |
このデータの中央値が第1四分位数になるので、\(154cm\)
同様に、中央値より右側のデータだけで考える。
| アンケートID | E3 | F1 | W7 | A0 | R9 |
| 身長(cm) | 173 | 176 | 178 | 179 | 180 |
このデータの中央値が第3四分位数になるので、\(178cm\)
四分位範囲とは?
まず、データの範囲とは、\((最大値)-(最小値)\) のことです。
データがどの広さで分布しているかを示します。
しかし、データの範囲だけでは少しデータが足りません。
データの範囲が同じでも、中央値にぎゅっと集まったデータと、全体的にバラバラなデータでは、分析結果が変わっているべきです。
このように、どれくらいデータがバラついているかを示すのが四分位範囲です。
データのばらつきの示し方は様々ですが、四分位範囲は \((第3四分位数)-(第1四分位数)\) で表現することになっています。
3種類の中央値の最大・最小の差を比べるイメージです。
次のデータについて、四分位範囲を求めよ。
(1) 7人の生徒が跳び箱のテストで跳んだ段数
| 生徒名 | A | B | C | D | E | F | G |
| 段数(段) | 5 | 6 | 6 | 7 | 7 | 8 | 9 |
(2) 8人の生徒における50m走の記録
| 生徒名 | い | ろ | は | に | ほ | へ | と | ち |
| 秒数(秒) | 6.4 | 6.9 | 7.2 | 7.4 | 7.6 | 8.0 | 8.1 | 8.9 |
(3) 道端で見かけた11人の身長の記録
| アンケートID | F1 | P5 | Q2 | B4 | R9 | A0 | E3 | W7 | N6 | S8 | C2 |
| 身長(cm) | 176 | 167 | 154 | 172 | 180 | 179 | 173 | 178 | 150 | 145 | 165 |
ちなみに、これらのデータは前回の例題で扱ったものと完全に同じものです。
四分位数などは、前問で求めたものをそのまま使ってしまいましょう。
(1) 前問より、第1四分位数は \(6段\) で、第3四分位数は \(8段\) だから、引き算して \(2段\)
(1) 前問より、第1四分位数は \(6.65秒\) で、第3四分位数は \(8.05秒\) だから、引き算して \(1.4秒\)
(1) 前問より、第1四分位数は \(154cm\) で、第3四分位数は \(178cm\) だから、引き算して \(24cm\)
箱ひげ図
箱ひげ図は、四分位範囲を箱で表し、最大値と最小値をひげで表現する図のことです。
詳しい作り方は、次の記事で紹介していますので、ぜひ読んでください。
まとめ
いかがだったでしょうか?
今回は覚えることばかりで大変でしたね。
しかし、今回の内容は全て箱ひげ図を作成するための前準備に他なりません。
多少知識が曖昧でも、次の箱ひげ図のセクションに進んで全体像を掴み、そこで理解するのがおすすめです。
一度で理解しようとしなくて大丈夫。
次の記事でお会いしましょう!



コメント