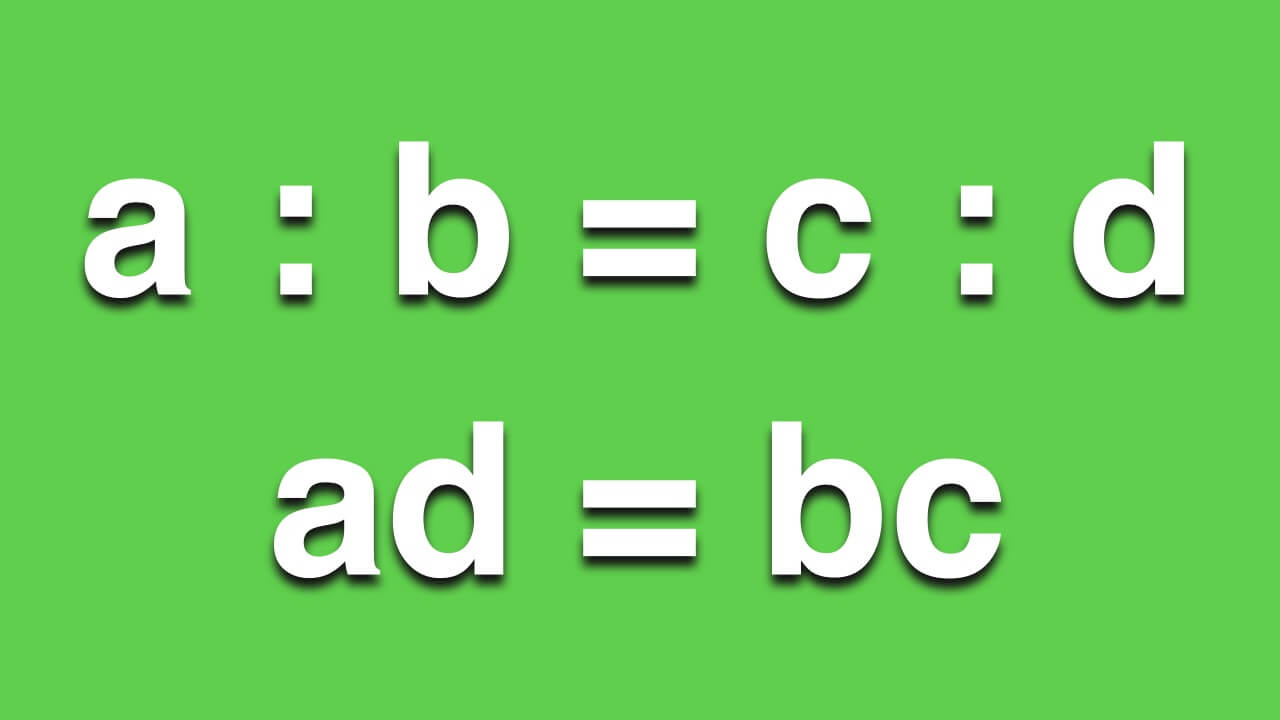
こんにちは。Daddyです。
今回は『比例式』というものを扱います。
“比例”式と言っても、\(y=3x\) のような比例のグラフを表すのことではありません。
あとで解説しますが、\(3:x=y:2\) のような式のことを言います。
比例式はさまざまな場面で登場する超超超キホン事項でありながら、あまり本質を理解せずにうまく活用できない人も多いです。
その原因の一つとして、教科書では『一次方程式』の分野で少ししか扱われないことにあります。
そもそも比例式は方程式とは異なるものですし、汎用性が非常に高いので、他分野で使えなくなりがちなのです。
この記事で『比例式』だけを重点的に学習することで、応用力を身につけていきましょう!
比例式とは
比例式とは、比の形で表された等式のことです。
比は小学生でも習った通り、:の記号を使って表される量の割合ですね。
次のような式は、すべて比例式です。
$$2:4=3:6$$ $$5:2:7=65:26:91$$ $$a:b=c:d$$
ここまでは、比例式という単語の確認です。
くれぐれも、関数の『比例・反比例』とごちゃ混ぜにしないように。
分数での表現
小学校でも習っているかもしれませんが、比例式の特徴として、比は分数に変形できるということが挙げられます。
これは、比がもともと複数の量の割合を示すものであり、分数でも割合を表現できるからです。
ここで、頭の良い人に向けて『一般に、\(a:b=c:d \iff \dfrac{a}{b}=\dfrac{c}{d}\)です』と説明しても良いですが、ややイメージしづらい……
ここでは具体的に、例題を解いて理解してみましょう。
次の比例式を分数の等式に変形して表せ。ただし、本例題において扱われる文字 \(a, b\) は0ではない。
(1) \(2:9=7:a\)
(2) \(b:2=3:b\)
(1) 分数に変形すると、次のようになる。$$2:9=7:a$$ $$\dfrac{2}{9}=\dfrac{7}{b}$$
このように、\(2:9\)を\(\dfrac{2}{9}\)に変形するといった、分母と分子の関係を覚えておくと良い。
なお、別解として、\(\dfrac{9}{2}=\dfrac{b}{7}, \dfrac{2}{7}=\dfrac{9}{b}\) などもある。
ちなみに、この後すぐのセクションを勉強すると、\(a=\dfrac{63}{2}\) と解くことができる。
(2) (1)と同様に変形する。$$b:2=3:b$$ $$\dfrac{b}{2}=\dfrac{3}{b}$$
別解は(1)と同様なので、省略。
ちなみに、中3数学を勉強すると、\(b=\pm\sqrt{6}\) と解くことができる。
内項の積・外項の積
ここで、内項の積と外項の積が等しくなるという性質を学んでいきます。
つまり、こういうこと。
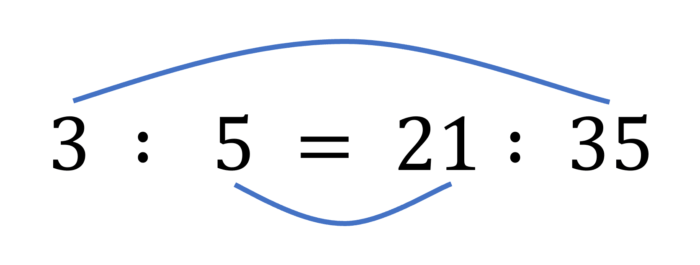
比例式において、内側同士をかけたもの(内項の積)と、外側同士をかけたもの(外項の積)は等しくなる。
実際にこの性質を使った問題を解くのは、次のセクションにしましょう。
ここでは、この性質が『一般に』正しいことを簡単に証明します。
つまり、すべての場合において正しいことを証明していきます。
$$a:b=c:d$$この式を分数表記に書き換えると、$$\dfrac{a}{b}=\dfrac{c}{d}$$分母を払うために、両辺に \(bd\) をかけて、$$\dfrac{a}{b} \times bd=\dfrac{c}{d} \times bd$$よって、$$ad=bc$$
これは内項の積・外項の積の形になっているから、題意は示された。
(証明終)
応用問題
ここからは、実際に問題演習に取り組みましょう。
ただ、中1数学の範囲は『一次方程式』のみなので、『相似』『式の値(高校数学)』は解けなくても構いません。
この2つを掲載したのは、『比例式=一次方程式』と思って欲しくなかったからです。
さまざまな場面で使われるということを念頭に、問題演習してください。
一次方程式
次の方程式を解け。$$8x:7=(9-x):2$$
比例式は割合を一目で理解することができますが、欠点としては、四則演算で数式を表現できていないことです。
内項の積・外項の積の関係を用いることで、いわゆる一次方程式のカタチに変形することができますね。
$$8x:7=(x+9):2$$内項の積と外項の積は等しいから、$$8x\times2=7\times(x+9)$$これを解いて、
\begin{eqnarray}
16x&=&7x+63\nonumber\\
9x&=&63\nonumber\\
x&=&7\nonumber
\end{eqnarray}
よって、\(x=7\)
相似
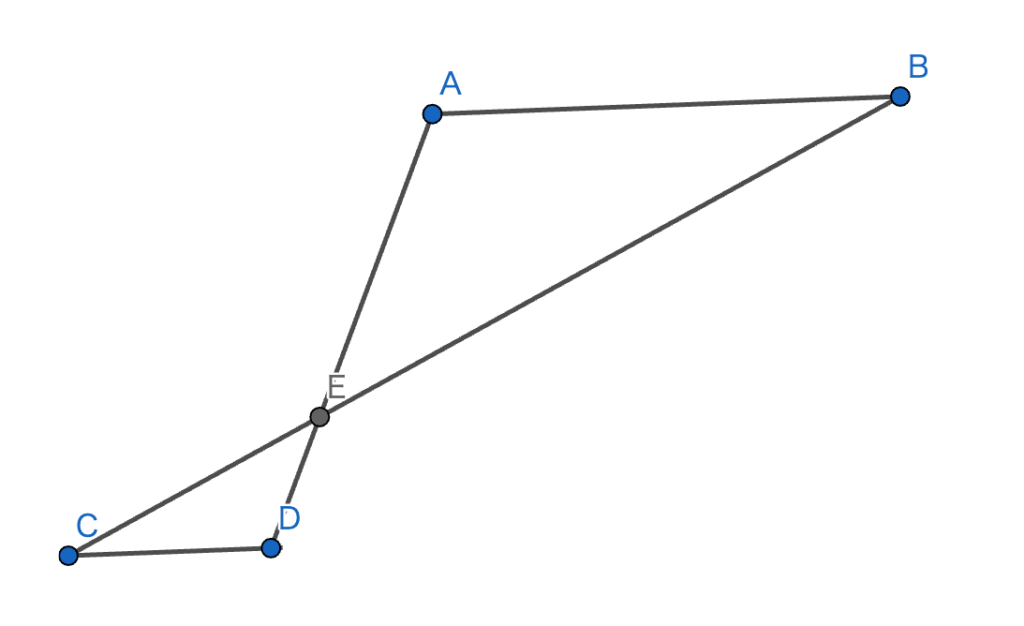
上の図形において、\(\triangle ABE \equiv \triangle DCE\) で、相似比は \(3:2\) である。 ここで、\(AE=7-x\) とすると、\(DE=x+2\) となるとわかっている。このとき、\(DE\) の長さを求めよ。
なお、上の図形は作問の都合上、正確でない。
\(\triangle ABE\) と \(\triangle DCE\) の相似比が \(3:2\) であるということは、\(AE:DE=3:2\) ということである。よって、
\begin{eqnarray}
(7-x):(x+2)&=&3:2 \nonumber\\
3 \times (x+2) &=& 2 \times (7-x) \nonumber\\
3x+6&=&14-2x \nonumber\\
5x&=&8 \nonumber\\
x&=&\dfrac{8}{5} \nonumber
\end{eqnarray}
ゆえに、\(DE\) の長さは、\(\dfrac{8}{5}+2=\color{red}{\dfrac{18}{5}}\)
式の値(高校数学)
次の等式が成り立つとき、\(\dfrac{x+y}{z}\) の値を求めよ。ただし、\(x+y+z \neq 0\) である。
\(\dfrac{x+y}{z}=\dfrac{y+z}{x}=\dfrac{z+x}{y}\)
『どこが比例式の問題なの?』と思った方もいるかもしれません。
実は、\(\dfrac{x+y}{z}=\dfrac{y+z}{x}=\dfrac{z+x}{y}\) を書き換えると次のような比例式に書き換えられます。
\((x+y):(y+z):(z+x)=z:x:y\)
分数式は \((分子):(分母)\)のカタチに書き換えられるのですね。
とはいえ、今回は比例式に書き換えたところでナニも見えてきません。
求めたい値、今回で言うなら \(\dfrac{x+y}{z}\) を、別の文字で置いてみましょう。
\(\dfrac{x+y}{z}=k\) と置く。
\(\dfrac{x+y}{z}=\dfrac{y+z}{x}=\dfrac{z+x}{y}=k\) となるから、次のように3つの式に分解し、分母を払うことができる。
\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=kz \\
y+z=kx \\
z+x=ky
\end{array}
\right.\notag
\end{eqnarray}
3つの式を縦にまとめて足すと、
\begin{eqnarray}
(x+y)+(y+z)+(z+x)&=&kz+kx+ky \nonumber\\
2(x+y+z)&=&k(x+y+z) \nonumber\\
\end{eqnarray}
問題文にあるように、\(x+y+z \neq 0\) だから、両辺を \(x+y+z\) で割って良いので、\(k=2\)
したがって、\(k=\color{red}{\dfrac{x+y}{z}=2}\)
このように、複数の文字が使われていて、分数のカタチになっている比例式は、とりあえず \(k\) で置くと解けることが多いので、解法を覚えておくと良いですね。
まとめ
いかがだったでしょうか?
比例式は、名前が少し難しそうなだけで、全然難しいことはありません。
ちょっと高校数学をかじったりもしてみましたが、理解するというよりも、こんな解き方をする問題もあるのかあ、と参考にしてくれれば幸いです。(とはいえ、難関私立高校では出題されることも多くあるので、要注意です。)
復習をしっかりして、定着させていきましょう。
それではっ!



コメント