こんにちは。
Frontiesta代表のDaddyです。
今回は、組立除法というものを勉強しましょう。
記事にたどり着いた皆さんは、『組立除法って聞いたことはあるけど、よくわからない』という方でしょう。
この記事を読めば、誰でも確実に組立除法のやり方をマスターできます。

やり方だけ忘れたから、今すぐ知りたいよ!
という方は、このリンクからジャンプ!
それでは、Let’s go!
組立除法の雰囲気をつかむ
組立除法とは、数式をわり算するときに使える、ちょっとした計算テクニックのことです。
かけ算とたし算だけを用いることで、計算ミスを極限まで減らすことができます。
唯一注意すべきなのは、割る方の式が(x-p)のカタチになっていなくてはならないこと。
ただ、この部分はあとでしっかりと解説します。
例えば、次のような問題を解くときに使います。
\(2x^5+x^4-5x^3+7x-9\) を \(x-2\) で割った商と余りを求めよ。

え?これってただの『整式の除算』じゃないの?

そうそう。ただ、めんどくさいやろ?今回勉強するのは、この計算の裏ワザっていうわけ。
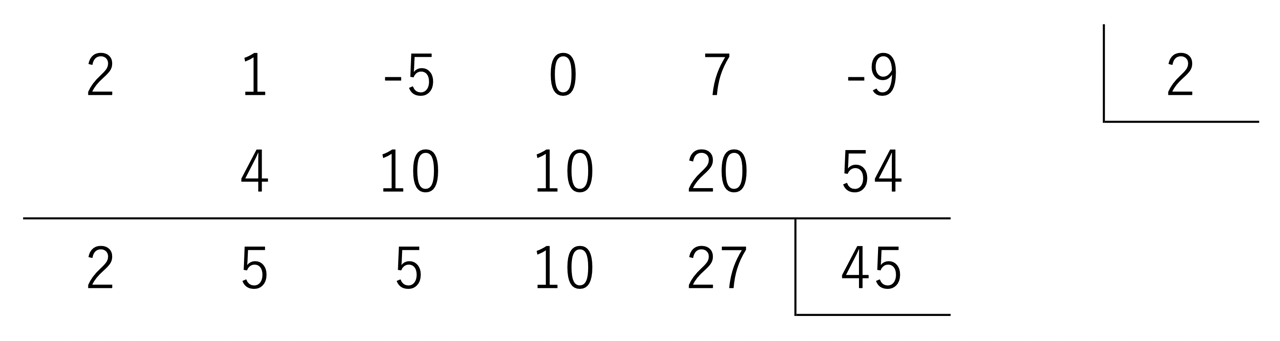
最終的には、次のような計算ができるようになるのが目標です!
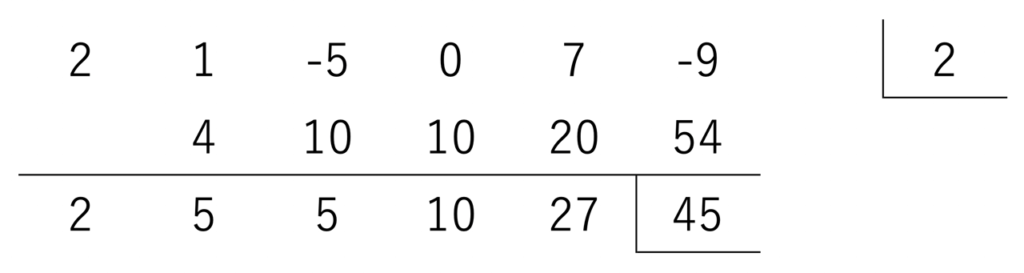

『整式の除算』で習った筆算とぜんぜん違うじゃん!でも、たし算の筆算には似ているような…

ええこと言うやん。組立除法の最大のポイントは、たし算やな。
組立除法の長所・短所
組立除法を勉強する最大のメリットは、計算がめっちゃ速いことです。
実際には、普通にわり算の筆算をしてしまっても答えはしっかりと出ます。
覚えていない人も結構います。
でも、組立除法を覚えておけば、計算ミスする可能性をぐっと減らして素早く計算できるのです。
例えば、次の例題を見てみましょう。
まずは、整式の除算の復習です。
\(2x^5+x^4-5x^3+7x-9\) を \(x-2\) で割った商と余りを求めよ。

さっきの問題だね。まずは普通に筆算してみるよ。
筆算のやり方を覚えていない人は、今すぐ下の記事をチェック!
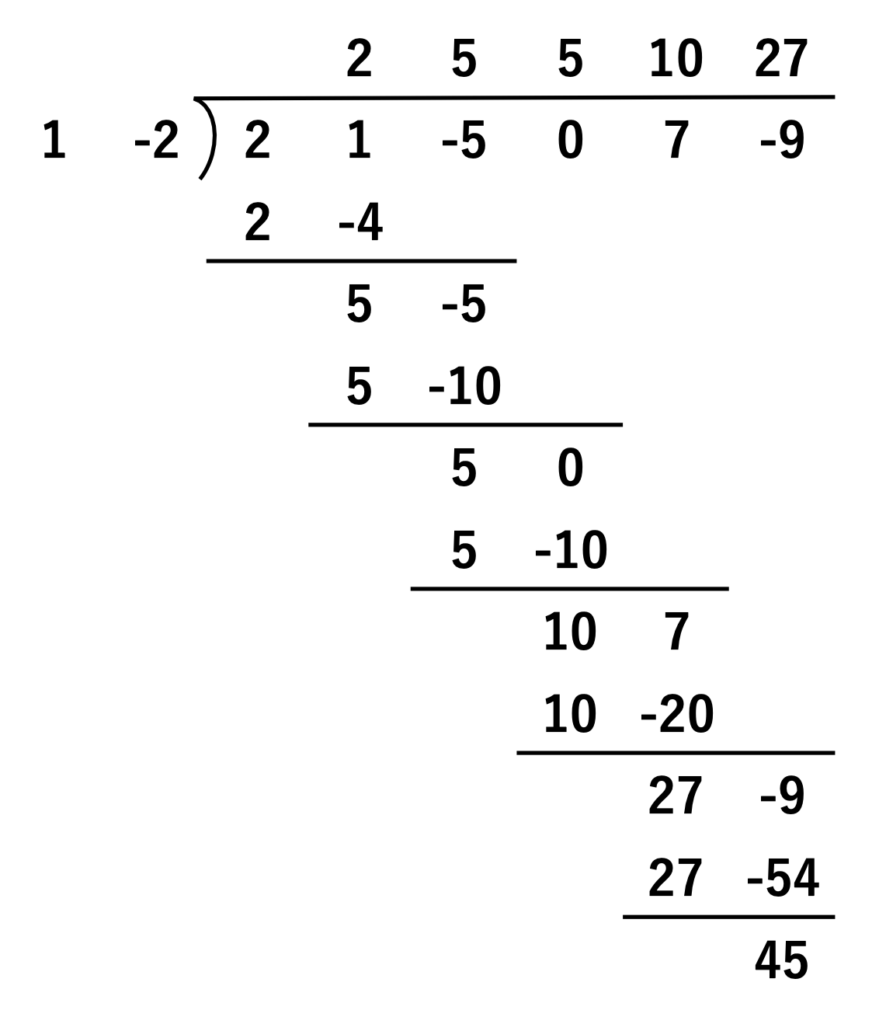

お、思ってたより大変じゃないか?

これ、係数だけで計算したからまだ楽なんやで。

係数だけの筆算を知らない人は、とてつもなく大変なんだろうな…
ということで、組立除法という素晴らしい計算法が編み出されました!
実は、組立除法も、やることは筆算と変わりません。
ただ、筆算のありとあらゆる部分を省略していきます。
実際に書くのは、問題文で与えられた青い部分と、実際に計算する赤い部分だけ。
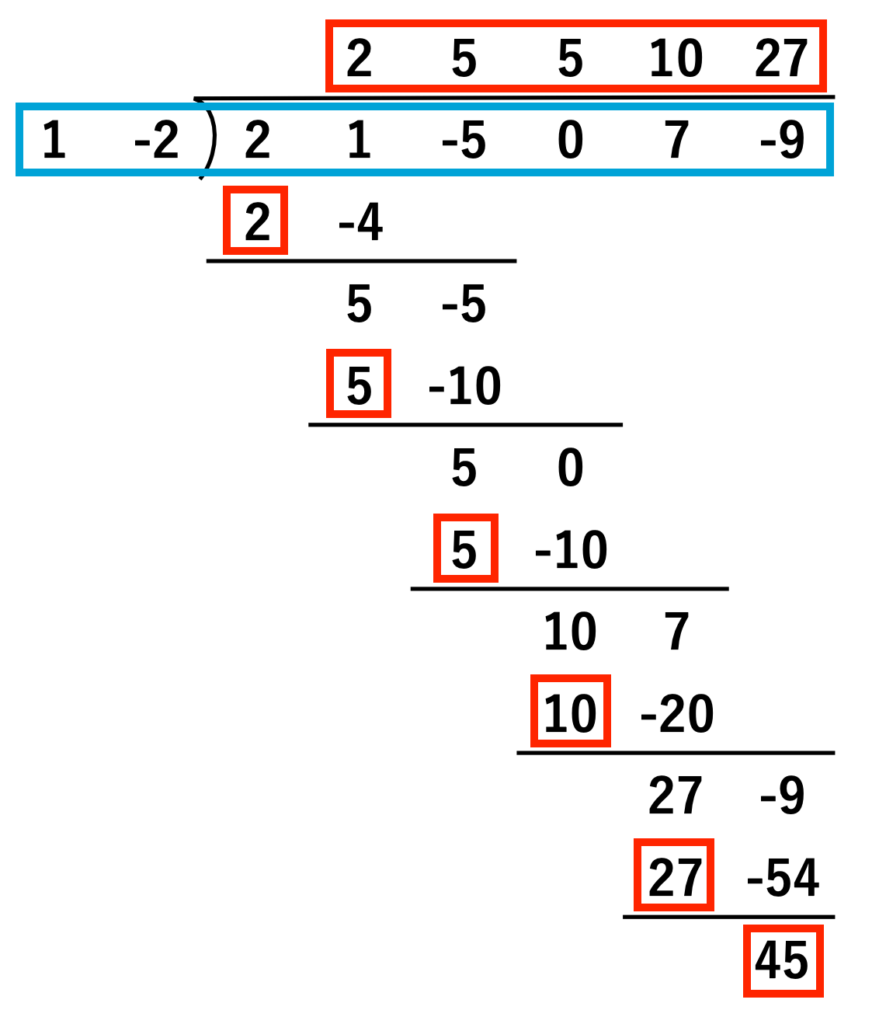

半分くらい省略できるじゃん!

なんせ組立除法は、ある特別なときにしか使えない裏技やからな。

え?もう一回言ってみ?

実は、組立除法が使える場面は限定的。使えないことも多いねん。
実は、割る整式が1次式かつ、\(x-p\) のカタチに変形してからでないと使えません。
割られる整式はぶっちゃけどうでもいいんですけど。
\(x-3, x+6, x+\dfrac{3}{2}\) などが、組立除法で使える例。
\(x\) の係数が1ということ。
\(2x-5\) なんかを組立除法で使いたい時は、式の全体を2で割って、\(x-\dfrac{5}{2}\) としなければなりません。
覚えておきましょう。
組立除法の計算法
それでは、計算法を伝授します!
さっきの例題を使いましょう。
\(2x^5+x^4-5x^3+7x-9\) を \(x-2\) で割った商と余りを求めよ。
まず、割られる整式と、2つの図形をセットしましょう。
こんな感じ。
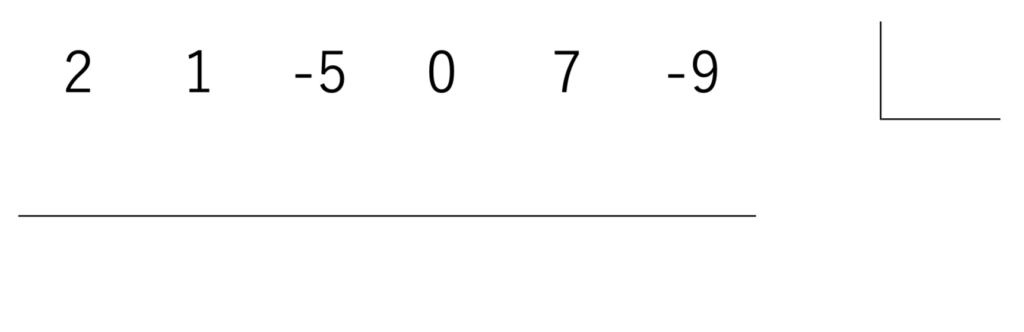
ここでは、割られる整式の係数だけを書いています。
右側の『カックン』が気になりますね。
ここには、割る整式 \(x-p\) の \(p\) をぶっ込みます。
今回なら、\(x-2\) の2をぶっ込みます。
なぜかというと、今後の計算でひき算を使わないため。
ほとんどの場合、ひき算よりたし算の方が楽でしょ?
マイナスに変形してからでないと使えないことには注意です。
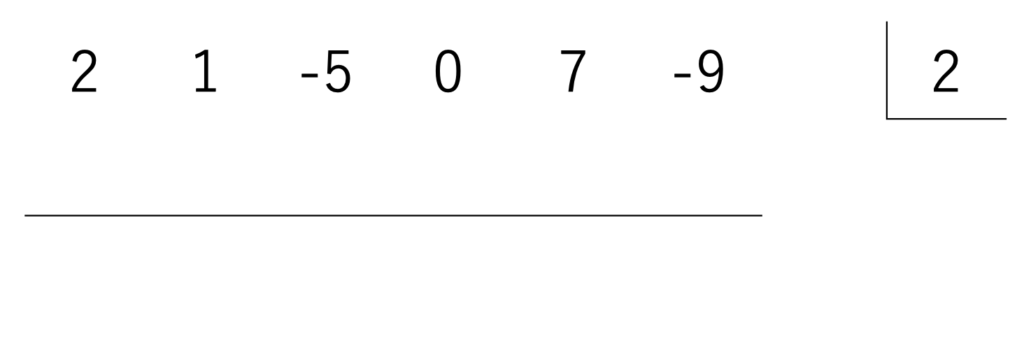
そして、イチバン左の数である2をそのまま下ろします。
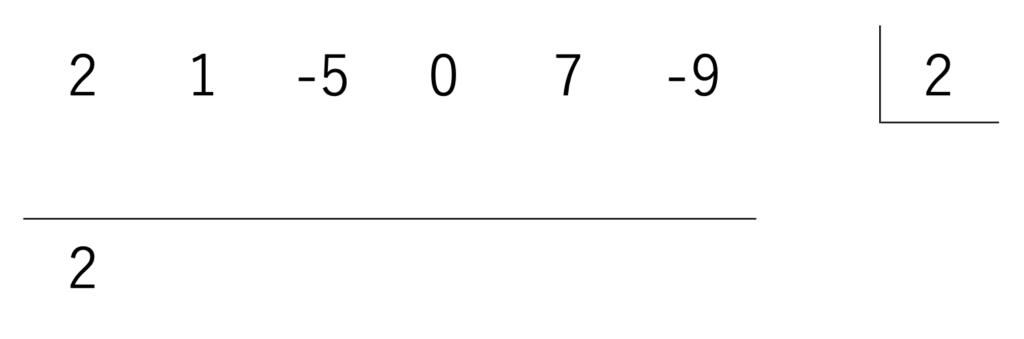
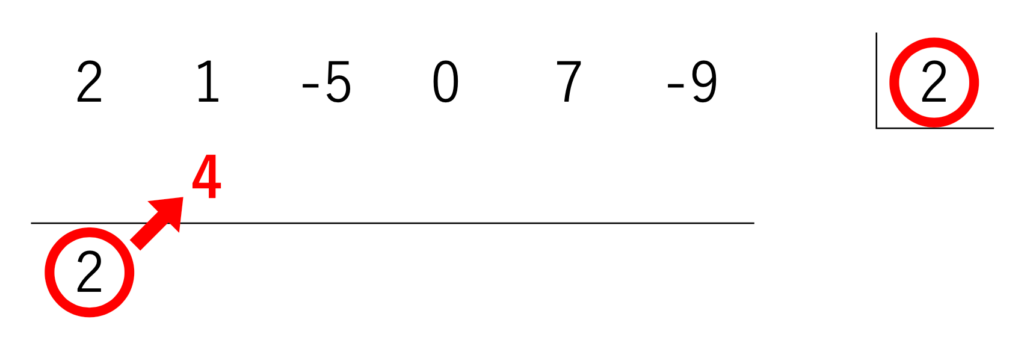
ここからが本番。
『斜めにかけ算、縦たし算』と唱えながら、地道に計算します。
まずはかけ算。
2つの赤丸をかけ算して、斜め上に記入します。
次はたし算。
縦をそのままたし算しましょう。
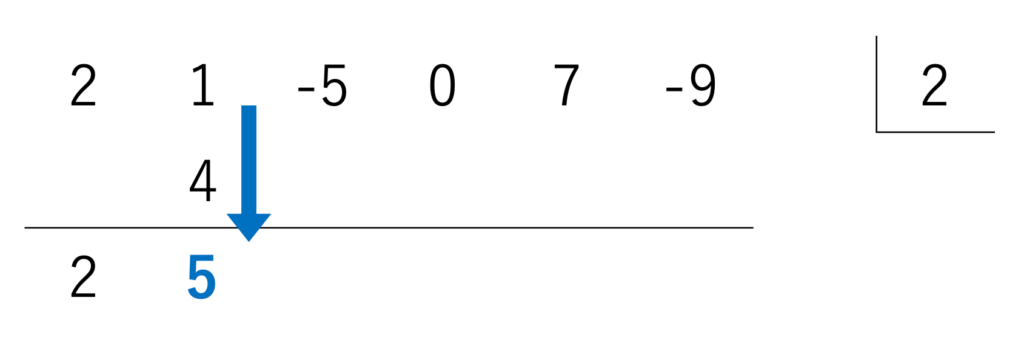
実際に繰り返すと、下のような図になります。
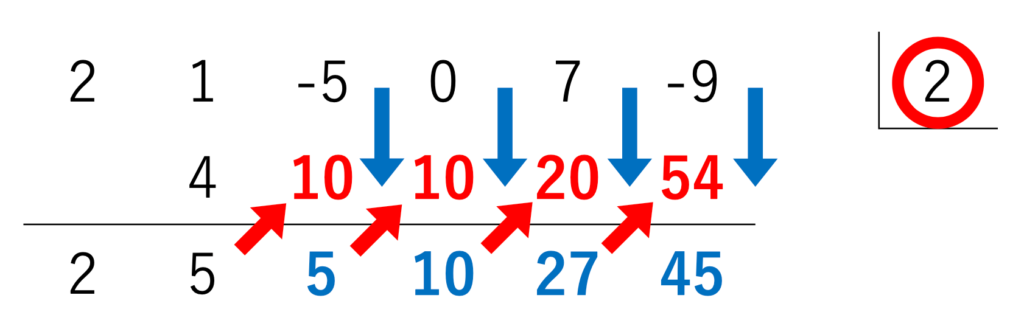
イメージつきますかね。
かけ算の筆算をやっているイメージです。
さあ、これで計算は完了。
余りが右下に、商が緑色のところに現れています。
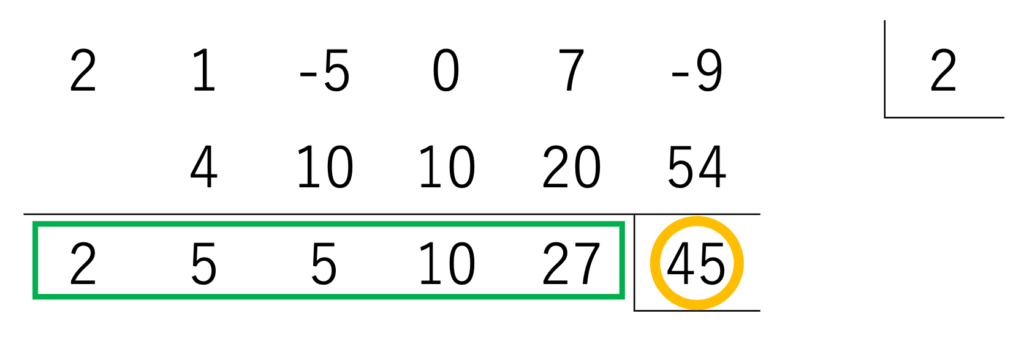
よって、商は \(2x^4+5x^3+5x^2+10x+27\) で、余りは \(45\) となります。
- 割られる整式をセット
- \(x-p\) の \(p\) をセット
- 左端を下ろす
- 『斜めにかけ算、縦たし算』
- 4を繰り返したら完成!
組立除法の証明
なぜ組立除法が成り立つのか、疑問に思う人もいるかもしれません。
証明自体はかなり地味で、『証明』と言えるほどのものでもないのですが…
しかも文字が多くなって見にくくなりますし。
そのため、無理して読むことはおすすめしません。
今回は、3次式の場合のみ証明しますが、一般に何次式でも成り立ちます。
\(ax^3+bx^2+cx+d\) を \(x- \alpha \) で割る。\((a \neq 0)\)
この時の商を \(px^2+qx+r\) 、余りを \(s\) と置く。
従って、次のような \(x\) についての恒等式が成立する。
\(ax^3+bx^2+cx+d=(x- \alpha)(px^2+qx+r)+s\)
係数を比較すると、\(a,b,c,d\) は次のように表せる。
\begin{eqnarray}
\left\{
\begin{array}{l}
a=p \\
b = q-p \alpha \\
c = r-q \alpha \\
d = s-r \alpha
\end{array}
\right.\notag
\end{eqnarray}
変形すると、\(p,q,r,s\) は次のように表せる。
\begin{eqnarray}
\left\{
\begin{array}{l}
p=a \\
q = b+p \alpha \\
r=c+q \alpha \\
s=d+r \alpha
\end{array}
\right.\notag
\end{eqnarray}
\(p=a\) は、組立除法における初めの操作『左端の数をそのまま下ろす』に相当する。
以降の式は、『\(\alpha\) を斜めにかけて、その後縦にたし算する』操作に相当する。
よって、題意は示された。
まとめ
最後に気をつけるべきこと。
組立除法は『絶対に使える!』と確信できた時だけに使ってください。
整式の除算はあくまで『筆算』を使ってやるべきものです。
次のような問題で無理やり組立除法をやることもできますが、それで計算ミスするくらいなら筆算した方が良いでしょう。
\(A\) を \(B\) で割った時の商と余りを求めよ。
\(A:-5x^4+8x^3-2x+1\)
\(B:3x-7\)
割る数のカタチが \(x-p\) になっていないでしょう?
こういった問題は、素直に筆算してください。
これで組立除法の解説は終わりです。
組立除法のやり方が不安になったら、またFrontiestaのサイトに戻ってきてくださいね。
それではっ!




コメント