
こんにちは。Daddyです。
今回は中3数学の超キホンである『展開』を扱います。
キホンとはいえ、決して簡単な内容ではなく、暗記すべき重要項目もてんこもり。
手を動かして覚えることを念頭に問題演習に取り組みましょう!
スマホでこの記事を閲覧している場合、数式が枠内に入りきっていないことがあります。スクロールをお試しください。
展開とは
展開とは、かけ算の式をたし算の式に変形することです。
例えばこんな感じ。
例)\((2x+3)(x-1)=2x^2+x-3\)
「これ、合ってるの?」というのはさておき、こんな感じで文字を含むかけ算の式を、単項式のたし算の形で表していくイメージです。
よく考えると、これまでは多項式の計算ではたし算とひき算しか扱ってきませんでした。
『展開』を勉強することで、かけ算もできるようになるのです。
※ 多項式の除法(わり算)は高校数学の範囲になります。興味のある方は、数学Ⅱ「整式の除法」を調べてみてください。
分配法則
分配法則は、小学生で習った展開の方法です。
以下の例題で、やり方を見直してみましょう。
次の式を単項式の和の形で表せ。
(1) \(4ab(2a-3b)\)
(2) \((x+2)(x-6)\)
(1)この式は、\(A(B+C)\)みたいな形になっています。
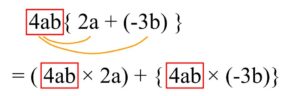
このように、分配法則を使って展開してあげると良いですね。
\((4ab \times 2a)+{4ab \times (-3b)}\)
\(=8a^2b-12ab^2\)
よって求める式は \(8a^2b-12ab^2\)
(2)この式はやや複雑。置換する必要があります。
\(A=x+2\)と置くと、
\((x+2)(x-6)=A(x-6)\)となるから、
\(A(x-6)=Ax-6A\)
\(A=x+2\)をもとの式に代入して、
\((x+2)x-6(x+2)\) ←\(A=x+2\)を代入
\(=x^2+2x-6x-12\)
\(=x^2-4x-12\)
よって求める式は\(x^2-4x-12\)
小学校で習った分配法則との違いは、置換する問題があるということです。
ただ、いちいち置換して展開するのもめんどくさい…
そこで、この置換によって得られる計算結果を根拠に、次のように展開することが許されています。
下の通りに分配して良い
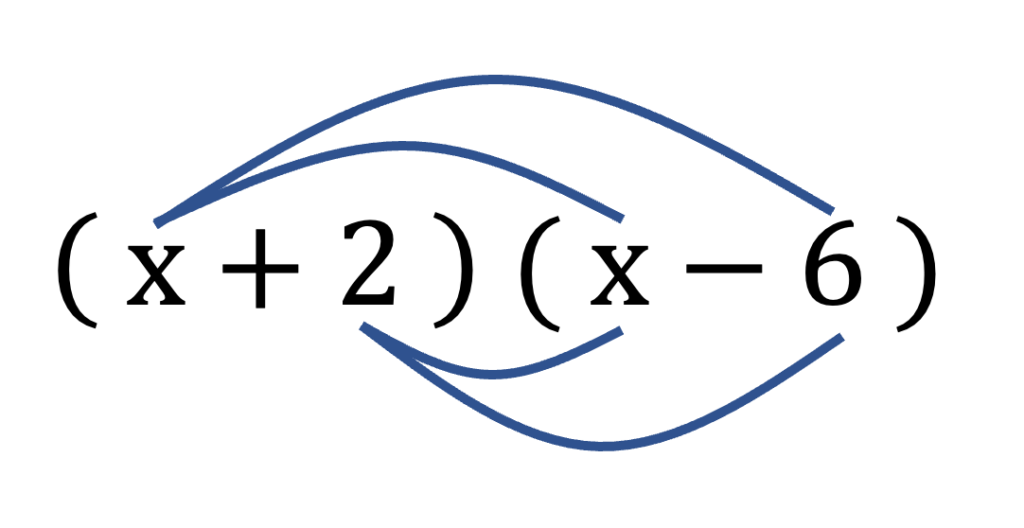
\((x+2)(x-6)\)
\(=x^2-6x+2x-12\)
\(=x^2-4x-12\)
こちらの方がラクかな?
この後説明する『乗法公式』ですが、忘れてしまった時はこの方法で展開すれば導出することができます。
計算はやや遅くなるものの、応用が効く手法ですので、必ず習得しておくように!
乗法公式
乗法公式について勉強します。
前問の⑵では置換を勉強しましたが、これだけではやや不十分。
というより、全ての問題でこんなことをしていたら、とんでもない時間がかかります。
そこで、特定のカッコがついた式に関しては答えを覚えてしまおうというわけ。
\((x+a)(x+b)=x^2+(a+b)x+ab\)
\((a+b)^2=a^2+2ab+b^2\)
\((a-b)^2=a^2-2ab+b^2\)
\((a+b)(a-b)=a^2-b^2\)
……覚えられるかいっ!
ちなみに証明は簡単。頑張って置換して展開するだけです。
こういった計算に関する公式は『日本語に翻訳して覚える』のが原則です。
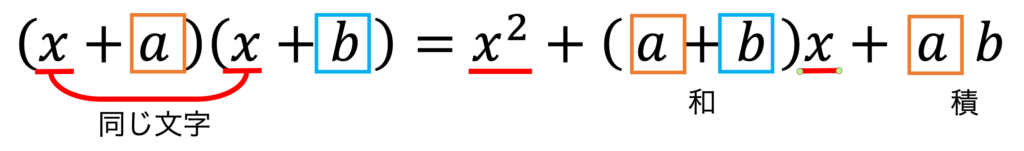

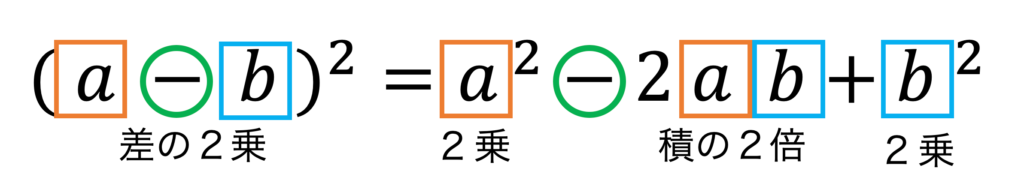

上の公式は、問題を解くたびに日本語で理解することで、そのうち瞬時に答えが求められるようになります。
小学生が筆算の練習を何度もするように、中学生は展開の練習を何度もする必要があります。
次の式を単項式の和の形で表せ。
(1) \((x+3)(x-2)\)
(2) \((x+5)^2\)
(3) \((x-1)^2\)
(4) \((x+4)(x-4)\)
(1) これは\((x+a)(x+b)\)のカタチ。\(a=3, b=-2\)とみなして、
\((x+3)(x-2)\)
\(=x^2+\{(3+(-2)\}x+3 \times (-2)\)
\(=x^2+x-6\)
よって\(x^2+x-6\)
(2) これは\((a+b)^2\)のカタチ。\(a=x, b=5\)とみなして、
\((x+5)^2\)
\(=x^2+2 \times 5 \times x+5^2\)
\(=x^2+10x+25\)
よって\(x^2+10x+25\)
(3) これは\((a-b)^2\)のカタチ。\(a=x, b=1\)とみなして、
\((x-1)^2\)
\(=x^2-2 \times 1 \times x+1^2\)
\(=x^2-2x+1\)
よって\(x^2-2x+1\)
(4) これは\((a+b)(a-b)\)のカタチ。\(a=x, b=4\)とみなして、
\((x+4)(x-4)\)
\(=x^2-4^2\)
\(=x^2-16\)
よって\(x^2-16\)
発展的な乗法公式
中学校では発展事項として扱われる公式をまとめました。
1つ目の公式は、『因数分解』の『たすきがけ』で学習することになると思います。
2つ目の公式は、数検などで問われることが多い印象です。
\((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)
\((a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
これは式を凝視しても理解しづらい公式です。例題を通して、具体的に計算する方法を身につけましょう。
次の式を単項式の和の形で表せ。
(1) \((2x-1)(3x-5)\)
(2) \((2x+y-3z)^2\)
(1) これは\((ax+b)(cx+d)\)のカタチ。
\((2x-1)(3x-5)\)
\(=(2 \times 3)x^2+\{2(-5)+(-1)3\}x+(-1)(-5)\)
\(=6x^2-13x+5\)
よって \(6x^2-13x+5\)
(2) これは\((a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\)のカタチ。
\((2x+y-3z)^2\)
\(=(2x)^2+(y)^2+(-3z)^2 + 2(2x)(y) + 2(y)(-3z) + 2(-3z)(2x)\)
\(=4x^2+y^2+9z^2+4xy-6yz-12zx\)
よって \(4x^2+y^2+9z^2+4xy-6yz-12zx\)
項をアルファベット順にしなくても良いの?と思った方へ。
結論からいうと『このままの方が良い』です。
3つの文字が使われていて、各項の次数がそろっている(今回は全ての項が2次)場合には、サイクリックの順(輪環の順ともいいます)で書き表すことが望ましいです。
\(x^2, y^2, z^2, xy, yz, zx\)の順に、x, y, zがくるくる回るようなイメージで記述しましょう。
まとめ
以上、展開の公式たちでした。
基本的な4つの公式たちは定期テストで頻出なだけでなく、必要最低限の計算能力として、さまざまな問題で必要となります。
発展的な2つの公式たちは、難関高校を受験する場合には必須の知識です。置換して求めることもできますが、かなり時間がかかってしまうものを厳選したので、覚えることが欠かせません。
問題演習を重ねることで、着実に計算スピードを上げていきましょう!



コメント