こんにちは、popoikです。
今回は連立方程式について説明したいと思います。
その前に、この記事では一次方程式が必須になります。
少しでも不安のある人は下の記事をご覧ください。(露骨な宣伝)
連立方程式とは
連立方程式とは複数の方程式が組み合わさってできた方程式のことです。わかりにくいですが、視覚的に表すと…
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 5y = 8 \\
11x + 19y = 30
\end{array}
\right.\notag
\end{eqnarray}
連立方程式では、上の式が両方成立する場合のxとyの値を求めます。
連立方程式の解き方
連立方程式はどの方法で解いても、大まかに言えば手順は同じです。
- 変数が一つの方程式を作る
- 1の方程式を解く
- 2の解をどちらかの式に代入する
- もう一方の解を求める
全ての連立方程式は基本的にこの手順で解いていきます。
加減法
多くの連立方程式はこの加減法で解くことになると思います。
加減法には4つの手順があります。
- 2つの式を掛け算を持ちいて1つの変数の係数をそろえる
- 2つの式を足したり引いたりすることで、2つの変数のうち1つを消去
- できた方程式を解き、方程式に代入する
- もう一方の解を求める
次の連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 5y = 19 …(1)\\
2x + 11y = 28…(2)
\end{array}
\right.\notag
\end{eqnarray}
解説
\begin{flalign}
&xの係数をそろえるために(1)を2倍(2)を3倍する&\nonumber\\
&\left\{%
\begin{split}
&6x + 10y = 38…(3)&\nonumber\\
&6x + 33y = 84…(4)\nonumber&
\end{split}
\right.\notag\\
&(4)-(3)をする。&\nonumber\\
&23y=46&\nonumber\\
&y=2&\nonumber\\
&yに2を代入する。&\nonumber\\
&6x+20=38&\nonumber\\
&x=3&\nonumber\\
&A x=3,y=2&\nonumber
\end{flalign}
代入法
代入法を用いるときは、y=2x+5のように一次関数の式の形が多いです。
手順としては
- 式を代入して、変数が1つの方程式を作って解く
- その解を代入してもうもう一方の変数の一次方程式を作って解く
次の連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
y = 2x + 12 …(1)\\
2x + y = 16…(2)
\end{array}
\right.\notag
\end{eqnarray}
解説
(1)の\(2x+12\)を(2)の\(y\)に代入する
\begin{flalign}
&\begin{split}
2x+(2x+12)&=&16\\
4x&=&4\\
x&=&1
\end{split}&\nonumber
\end{flalign}
(1)に\(x\)を代入する。
\begin{flalign}
&\begin{split}
y&=2+12\\
y&=14
\end{split}&\nonumber
\end{flalign}
$$x=1,y=14$$
2つの解き方の使い分け
連立方程式には上記のように2つの解き方を中学数学で使います。
それではどのように使い分ければよいのでしょうか。
・基本的には加減法を用いて解く
・代入法を用いるときにはぱっと見でわかるシグナル的なものがある。
例)y=の形で出題されている。
・関数の交点の問題の時は代入法を用いる。
3つ目について先程の例題で見ていきます。
次の連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
y = 2x + 12 …(1)\\
2x + y = 16…(2)
\end{array}
\right.\notag
\end{eqnarray}
この問題は、(2)を変形して、次のように考えられます。
\begin{eqnarray}
\left\{
\begin{array}{l}
y = 2x + 12 …(1)\\
y = -2x+16…(2)
\end{array}
\right.\notag
\end{eqnarray}
この一次関数の交点は…
\(2x+12=-2x+16\)
\(x=1\)
\(y=2+12\)
\(y=12\)
$$x=1,y=14$$
また、この式をグラフで表すと(1,14)で交わることがわかると思います。
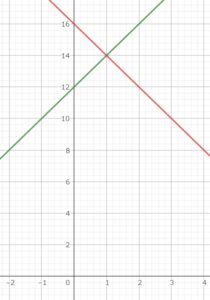
視覚的に解いてみるとイメージがしやすいと思います。
練習問題
以上の解き方を意識しながら次の問題を解いてみましょう。
次の連立方程式を解け
(1)1,1
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 3y = 5 \\
4x -3y = 1
\end{array}
\right.\notag
\end{eqnarray}
(2)9,-5
\begin{eqnarray}
\left\{
\begin{array}{l}
5x + 7y = 10 \\
15x + 20y = 35
\end{array}
\right.\notag
\end{eqnarray}
(3)1,7
\begin{eqnarray}
\left\{
\begin{array}{l}
y=2x+5 \\
y=x+6
\end{array}
\right.\notag
\end{eqnarray}
(4)1,7/2
\begin{eqnarray}
\left\{
\begin{array}{l}
2y = 2x+5 \\
6x + 4y = 20
\end{array}
\right.\notag
\end{eqnarray}
次の連立方程式を解け
(1)1,1
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 3y = 5…(1) \\
4x -3y = 1…(2)
\end{array}
\right.\notag
\end{eqnarray}
(1)+(2)をして\(y\)を消去する。
\(6x=6\)
\(x=1\)
\(x\)に1を代入する。
\(2+3y=5\)
\(y=1\)
$$x=1,y=1$$
(2)9,-5
\begin{eqnarray}
\left\{
\begin{array}{l}
5x + 7y = 10…(1) \\
15x + 20y = 35…(2)
\end{array}
\right.\notag
\end{eqnarray}
(1)×3-(2)をして\(x\)を消去する。
\(y=-5\)
\(y\)に-5を代入する。
\(5x-35=10\)
\(x=9\)
$$x=9,y=-5$$
(3)1,7
\begin{eqnarray}
\left\{
\begin{array}{l}
y=2x+5…(1) \\
y=x+6…(2)
\end{array}
\right.\notag
\end{eqnarray}
(1)と(2)がともに\(y=\)の式で表されているから、
\(2x+5=x+6\)
\(x=1\)
\(x\)に1を代入する。
\(y=2+5\)
\(y=7\)
$$x=1,y=7$$
(4)1,7/2
\begin{eqnarray}
\left\{
\begin{array}{l}
2y = 2x+5…(1) \\
6x + 4y = 20…(2)
\end{array}
\right.\notag
\end{eqnarray}
(2)を\(×\frac{1}{2}\)して、(1)を(2)に代入する。
\(3x+2x+5=10\)
\(x=1\)
\(x\)に1を代入する。
\(2y=2+5\)
\(y=\frac{7}{2}\)
$$x=1,y=\frac{7}{2}$$
まとめ
連立方程式を解くには主に加減法と代入法があり、使い分けが大切です。
・基本的には加減法を用いて解く
・代入法を用いるときにはぱっと見でわかるシグナル的なものがある。
例)y=の形で出題されている。
・関数の交点の問題の時は代入法を用いる。
初めのうちはどちらを用いるべきか迷うと思いますが、たくさんの問題を解いて上手に使い分けられるようになりましょう。
それではまたどこかの記事で。





コメント