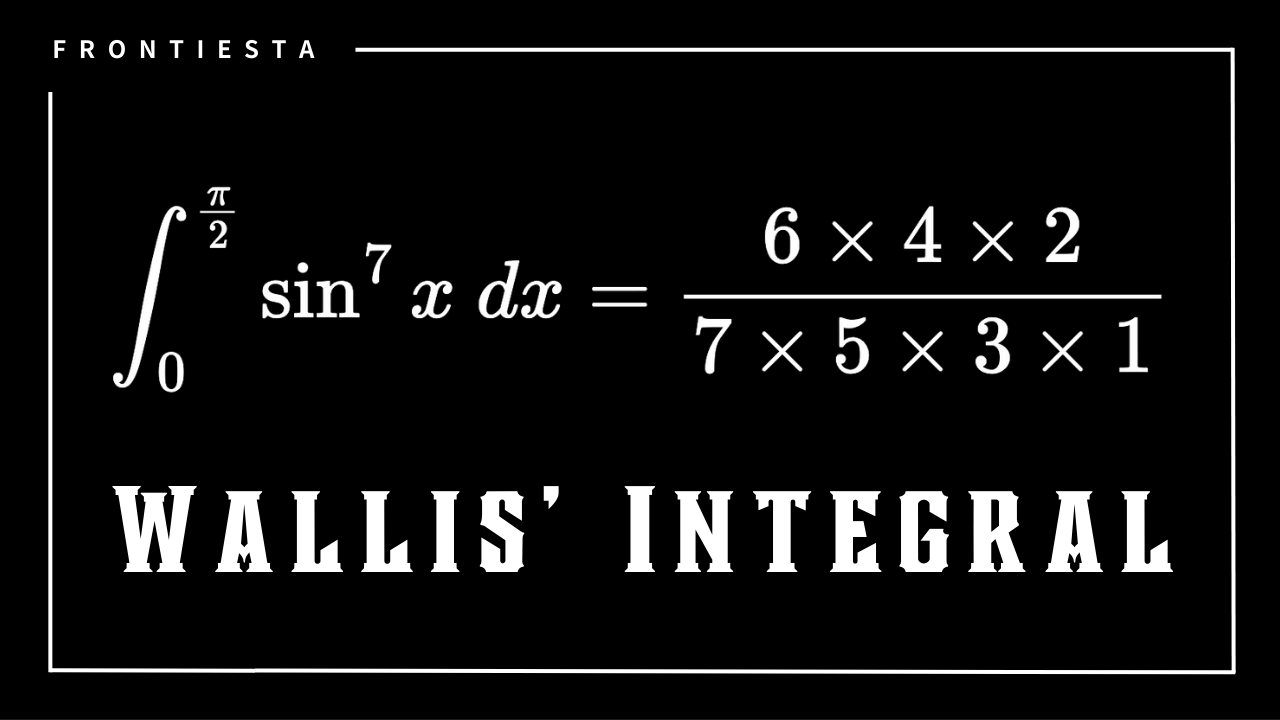

こんにちは。積分大好きDaddyです。
今回はウォリス積分を学習しましょう。
ウォリスさんの名前は一切覚えなくて構いませんw
が、積分の問題としては一、二を争うほど大切なもの。
『あらゆる積分のテクニックをマスターしたゼ』という猛者だけが、この記事を読むべきでしょう。
とはいえ、いつものように話し口調でわかりやすく解説していきます。
それでは早速、Let’s go!
ウォリス積分とは
意味はわからなくていいので、とりあえず結論から見ていきましょう。
ウォリス積分によると、こんなことがわかっています。
(\(!!\)という記号がありますが、後でしっかり解説するので逃げ出さないで!)
\(n=0, 1, 2, \cdots\) のとき、\(I_n\) を次のように定義する。
\(I_n = \displaystyle \int_0^{\frac{\pi}{2}} \sin^n x dx= \int_0^{\frac{\pi}{2}} \cos^n x dx\)
このとき、\(I_n\) の定積分の一般項が求まる。
\begin{eqnarray}
I_n =
\begin{cases}
\dfrac{(n-1)!!}{n!!} \cdot \dfrac{\pi}{2} & (nが偶数)\\
\dfrac{(n-1)!!}{n!!} & (nが奇数)
\end{cases}\notag
\end{eqnarray}
ここで覚えて欲しいのは、次の点です。
- \(0 \rightarrow \dfrac{\pi}{2}\) の定積分である!
- \(n\) が偶数か奇数か、で答えが変わる!
- \(\sin ^n x\) も \(\cos ^n x\) も答えが一緒!
- 証明には、部分積分を使う!
ひとまず、飲み込んでいただけたでしょうか?
それでは、ここからは誘導付きの例題を解きながら、ステップを踏んで証明していきます。
最後には、この公式の美しさも理解できるはず!
証明してみる
それでは、こんな例題を解いてみましょう。
自力で解くのはかなり難しいと思うので、解説を見ながら手を動かしてみてください。
\(n=0, 1,2,\cdots\) のとき、\(I_n\) を次のように定義する。
\(I_n = \displaystyle \int_0^{\frac{\pi}{2}} \sin^n x dx\)
(1) \(I_n=\dfrac{n-1}{n} I_{n-2}\) を証明せよ.
(2) \(I_0, I_1\) を求めよ。
(3) \(I_n\) を \(n\) の式で表せ。
(4) \(\displaystyle \int_0^{\frac{\pi}{2}} \sin^n x dx = \int_0^{\frac{\pi}{2}} \cos^n x dx\) を証明せよ。

き、きつい…
普通に入試問題っぽいオーラを感じる…

結構いろんな大学で出題されてるっぽいで。でも誘導に乗れば怖くない。
積分漸化式をつくる
まずは(1)を討伐しましょう!
まず覚えるべきことは、『漸化式は部分積分で作る!』です。
これは今回の記事で一番覚えて帰ってほしいこと。

\(\sin ^n x\) をどうやって部分積分するのさ?
手段はただ一つ。
なんとしてでも部分積分をしなくてはならないのですから…
\(\sin ^n x\) をバラして、\(\sin x \cdot \sin ^{n-1}x\) にしてやれば良いのですね。
解答は下のようになります。(長いので、折りたたんでいます)
下の数式は横にスクロールできます。
\begin{eqnarray}
I_n &=& \displaystyle \int_0^{\frac{\pi}{2}} \sin^n x dx \nonumber \\
&=& \displaystyle \int_0^{\frac{\pi}{2}} \sin x \cdot \sin ^{n-1}x dx \nonumber \\
&=& \displaystyle \int_0^{\frac{\pi}{2}} (- \cos x)’ \cdot \sin ^{n-1}x dx \nonumber \\
&=& \left[ – \cos x \cdot \sin ^{n-1}x \right] _0^{\frac{\pi}{2}} – \displaystyle \int_0^{\frac{\pi}{2}} – \cos x \cdot (\sin ^{n-1}x)’ dx \ (部分積分)\nonumber \\
&=& (0-0)+ \displaystyle \int_0^{\frac{\pi}{2}} \cos x \{ (n-1)\sin ^{n-2}x \cdot \cos x \} dx \nonumber \\
&=& (n-1) \displaystyle \int_0^{\frac{\pi}{2}} \cos ^2 x \cdot \sin ^{n-2}x dx \nonumber \\
&=& (n-1) \displaystyle \int_0^{\frac{\pi}{2}} (1- \sin ^2 x) \cdot \sin ^{n-2}x dx \nonumber \\
&=& (n-1) \left\{\displaystyle \int_0^{\frac{\pi}{2}} \sin ^{n-2}x dx \ – \displaystyle \int_0^{\frac{\pi}{2}} \sin ^n x dx \right\} \nonumber \\
&=& (n-1)(I_{n-2} \ – \ I_n)\nonumber \\
\end{eqnarray}
したがって、\(I_n = (n-1)(I_{n-2} \ – \ I_n)\)
これを整理すると、\(I_n=\dfrac{n-1}{n} I_{n-2}\)

ちょっと途中式が丁寧すぎたな…

実際に答えを書くときは、もう少し省略してもいいかもね。
一般項を出す
(2)(3)で漸化式を解いていきます。
もはや積分の問題じゃありませんw
まずは(2)の簡単そうな問題をチャチャっと討伐しましょうか。
\begin{eqnarray}
I_0 &=& \displaystyle \int_0^{\frac{\pi}{2}} \sin^0 x dx = \displaystyle \int_0^{\frac{\pi}{2}} 1 dx \nonumber\\
&=& \left[x \right]_0^{\frac{\pi}{2}} = \color{red}{\dfrac{\pi}{2}}\nonumber
\end{eqnarray}
\begin{eqnarray}
I_1 &=& \displaystyle \int_0^{\frac{\pi}{2}} \sin^1 x dx \nonumber\\
&=& \left[- \cos x \right]_0^{\frac{\pi}{2}}\nonumber\\
&=& – \cos \dfrac{\pi}{2} +\cos 0\nonumber\\
&=& \color{red}{1}\nonumber
\end{eqnarray}
漸化式で初項だけでなく、\(I_0, I_1\) ともに求めたのには、どうやら理由がありそうですね。
さて、お次は(3)。ちょいと難しいです。
ここで、nが十分に大きいと仮定します。
(1)で求めたように、\(I_n=\dfrac{n-1}{n} I_{n-2}\)
この式は、\(n, n-2, n-4, \cdots\) でも使えます。
すると、
\begin{eqnarray}
I_n&=&\dfrac{n-1}{n} I_{n-2} \nonumber\\
\nonumber\\
I_{n-2}&=&\dfrac{n-3}{n-2} I_{n-4} \nonumber\\
\nonumber\\
I_{n-4}&=&\dfrac{n-5}{n-4} I_{n-6} \nonumber\\
\nonumber\\
&\cdots& \nonumber
\end{eqnarray}
これらを \(I_n=\dfrac{n-1}{n} I_{n-2}\) の漸化式に順番に代入してみます。
すると、右辺の \(I_n\) の \(n\) の数が小さくなっていくではありませんか!
\begin{eqnarray}
I_n&=&\dfrac{n-1}{n} I_{n-2} \nonumber\\
\nonumber\\
&=&\dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} I_{n-4} \nonumber\\
\nonumber\\
&=&\dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} \cdot \dfrac{n-5}{n-4} I_{n-6}\nonumber\\
\nonumber\\
&\cdots& \nonumber
\end{eqnarray}
とはいえ、\(n\) も無限大なわけではありません。
いずれ \(4,3,2,1,0\) と順番に小さくなっていきます。
できる限り小さくすると、こうなることがわかるでしょう。
\(I_n = \cdots \dfrac{4}{5} \cdot \dfrac{2}{3} I_1\)
または
\(I_n = \cdots \dfrac{3}{4} \cdot \dfrac{1}{2} I_0\)

え、何で答えが2通りになってるの?

それは、\(I_n\) の \(n\) が2ずつ減っているから。

そっか。下のような具体例で考えるとわかりやすいね。
\begin{eqnarray}
I_7 = \dfrac{6}{7} \cdot \dfrac{4}{5} \cdot \dfrac{2}{3} I_1 \ (nが奇数の例)\nonumber\\
\nonumber\\
I_6 = \dfrac{5}{6} \cdot \dfrac{3}{4} \cdot \dfrac{1}{2} I_0 \ (nが偶数の例)\nonumber
\end{eqnarray}
あとはカンタン。
偶奇でパターン分けして答えを出せば良いのですね。
ここで、\(I_0, I_1\) は(2)で既に求めていることに注意!
nが奇数のとき
\begin{eqnarray}
I_n &=& \dfrac{n-1}{n} I_{n-2} \nonumber\\
\nonumber\\
&=& \dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} I_{n-4}\nonumber\\
&=& \cdots \nonumber\\
&=& \dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} \cdots \dfrac{2}{3} \cdot I_1\nonumber\\
\nonumber \\
&=& \color{red}{\dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} \cdots \dfrac{2}{3} \cdot 1}\nonumber\\
\end{eqnarray}
nが偶数のとき
\begin{eqnarray}
I_n &=& \dfrac{n-1}{n} I_{n-2} \nonumber\\
\nonumber\\
&=& \dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} I_{n-4}\nonumber\\
&=& \cdots \nonumber\\
&=& \dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} \cdots \dfrac{1}{2} \cdot I_0\nonumber\\
\nonumber \\
&=& \color{red}{\dfrac{n-1}{n} \cdot \dfrac{n-3}{n-2} \cdots \dfrac{2}{3} \cdot \dfrac{\pi}{2}}\nonumber\\
\end{eqnarray}

これで(3)は終わり!

いやー、確かに規則があって綺麗だけどさ…もっといい書き方ないの?

しゃあないな。最後に二重階乗を教えたろ。
忠告しておきますが、先ほどの解答で満点です。
もっと綺麗に書き表したい人に、\(!!\) の記号を伝授いたします。
\(!!\) の意味はズバリ、1個飛ばしの階乗です!
下が例となります。
\(8!! = 8 \times 6 \times 4 \times 2\)
\(11!!=11 \times 9 \times 7 \times 5 \times 3 \times 1\)
これを使えば、\(I_n\) は次のように表せますね。
分子と分母はそれぞれ、2ずつ減っているのがポイント。
\begin{eqnarray}
I_n =
\begin{cases}
\dfrac{(n-1)!!}{n!!} \cdot \dfrac{\pi}{2} & (nが偶数) \\
\dfrac{(n-1)!!}{n!!} & (nが奇数)
\end{cases}\notag
\end{eqnarray}

書く量、だいぶ減らせたね。

もう一度言うけど、二重階乗のカタチやなくても正解やで。
King Property
(4)はオマケみたいな問題。
King Propertyで一発です。
それより、『\(\sin\) でも \(\cos\) でも答えが変わらないんだ〜』という美しさに感動してください。
『King Propertyってナニ?』という人は、下の記事へGO!
それでは解答。
対称性より、一般に次のことが言える。(King Propertyという具体名を記述してはならない)
\(\displaystyle \int_a^b f(x) dx = \displaystyle \int_a^b f(a+b-x) dx\)
したがって、
\begin{eqnarray}
&\quad& \displaystyle \int_0^{\frac{\pi}{2}} \sin ^n x dx\nonumber\\
&=& \displaystyle \int_0^{\frac{\pi}{2}} \sin^n \left(0+ \dfrac{\pi}{2} \ – \ x \right) dx \nonumber\\
&=& \displaystyle \int_0^{\frac{\pi}{2}} \left\{ \sin \left(\dfrac{\pi}{2} \ – \ x \right)\right\}^n dx \nonumber\\
&=& \displaystyle \int_0^{\frac{\pi}{2}} \cos ^n x dx\nonumber
\end{eqnarray}
King Propertyを使わない方法ももちろんあります。
が、どう考えてもKing Propertyが使えそうなカタチなのですから、使うに越したことはないのです。
まとめ
いかがだったでしょうか?
ウォリス積分の証明がそのまま大問として扱われることもありますし、ちょっとした計算テクとして使うこともできます。
例えば、\(\displaystyle \int_0^{\frac{\pi}{2}} \cos ^4 x dx\) を計算したいとき。
今の皆さんならすぐに計算できますよね?
答えは、\(\dfrac{3}{4} \cdot \dfrac{1}{2} \cdot \dfrac{\pi}{2} = \dfrac{3}{16} \pi\)。
いちいち半角の公式を使って…みたいなことはしなくて良いわけ。
公式の導出から暗記まで、完ペキにしていきましょう!
それではっ!




コメント